• 二叉树与堆
  • 二叉树
    • 满二叉树
    • 完全二叉树
    • 二叉树的遍历
      • 前序遍历和中序遍历还原二叉树
      • 前序遍历和中序遍历还原二叉树
    • 排序二叉树
    • 一般树转为二叉树
  • 堆
    • 优先队列
    • 映射二叉堆
      • 常用操作的复杂度
  • 远征
  • 维护中位数
• 最短路
  • Floyd 算法
    • 概述
  • Dijkstra 算法
    • 单源最短路问题
    • 算法流程
    • 算法演示
  • Dijkstra算法的优化
    • 堆优化
  • SPFA 算法
    • SPFA 思想
    • 示例代码
  • 奶牛的比赛
  • 迷阵突围
  • 香甜的黄油
  • Nya Graph
  • 迷阵突围（二）
• 并查集
  • 并查集
  • 并查集的路径压缩
  • 网络社交
  • 关押罪犯
• 树上基础算法
  • 最小生成树
    • 生成树
    • 最小生成树
  • Kruskal 算法
    • 证明 Kruskal
  • Prim 算法
    • 核心代码
  • 最小生成树性质
  • 树的重心
    • 代码
  • 树的直径
• 不带权图算法
  • 拓扑排序
    • 排队问题
    • DAG
    • 求解排队问题
    • 拓扑排序
      • 参考代码
    • 拓扑排序的一些应用
  • 欧拉路与欧拉回路
    • 七桥问题
    • 欧拉图的判定
      • 欧拉图
      • 无向欧拉图的判定
      • 有向欧拉路的判定
    • 求解欧拉路径
      • 求解无向图欧拉路径
      • 求解有向图欧拉路径
• 图论建模
  • SPFA 判断负权环
  • 最短路建模方法总结
    • 算法选择
  • 最小生成树建模方法总结
  • 最小生成树建模
  • 次小生成树
    • 算法一：
    • 算法二：
    • 算法二：
    • 具体操作
• 基础树上 DP
  • 树上动态规划
  • 例题：奇怪的花卉
    • 解析
    • 参考代码
  • 树上的最小点覆盖
    • 解析
  • 按点计算贡献
    • [[NOIP 2014] 联合权值](https://www.luogu.com.cn/problem/P1351)
      • 解析
      • 参考代码
  • 按边计算贡献
    • 战后重建
      • 解析
      • 参考代码
  • 基础换根
    • 解析
• 区间动态规划
  • 区间 DP
    • 例题：[[USACO06FEB] 奶牛的零食](https://www.luogu.com.cn/problem/P2858)
      • 解析
      • 参考代码
    • 例题：合并石子
      • 解析
      • 参考代码
    • 破环成链
  • 区间 DP 记录路径
    • 例题：[[NOIP 2003] 加分二叉树](https://www.luogu.com.cn/problem/P1040)
      • 解析
      • 参考代码
• 算法的数据结构优化
  • 双端队列
  • 01 BFS
    • 电路维修
  • 中途相遇法
    • 例题：[[CEOI 2015] 冰球世锦赛](https://www.luogu.com.cn/problem/P4799)
      • 解析
      • 参考代码
• 记忆化搜索与 DAG 上的动态规划
  • 斐波那契数列
    • 记忆化搜索
  • [[NOIP2005] 采药](https://www.luogu.com.cn/problem/P1048)
  • 理解记忆化搜索与动态规划
  • 记忆化搜索实现区间DP
    • 例题《沙子合并》
      • 核心代码展示
  • DAG 上 DP
    • [[HAOI2016] 食物链](https://www.luogu.com.cn/problem/P3183)
      • 记忆化搜索解决 DAG 上 DP
        • 参考代码
      • 拓扑排序解决 DAG 上 DP
        • 参考代码

二叉树与堆

二叉树

二叉树是 $n(n\ge 0)$ 个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。

由二叉树定义以及图示分析得出二叉树有以下特点：

1. 每个结点最多有两棵子树，所以二叉树中不存在度大于 $2$ 的结点。
2. 左子树和右子树是 有顺序的，次序不能任意颠倒。
3. 即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。
4. 二叉树中，第 $i$ 层最多有 $2^{i-1}$ 个结点。
5. 如果二叉树的深度为 $K$，那么此二叉树最多有 $2^K-1$ 个结点。
6. 二叉树中，终端结点数（叶子结点数）为 $n_0$，度为 $2$ 的结点数为 $n_2$，则 $n_0=n_2+1$。

满二叉树

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

满二叉树的特点有：

1. 叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
2. 非叶子结点的度一定是 $2$。
3. 在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。

完全二叉树

一棵深度为 $k$ 的二叉树中，若前 $k-1$ 层为满二叉树，第 $k$ 层的结点连续分布在左边，该树为完全二叉树。

注：满二叉树是特殊形式的完全二叉树。

完全二叉树的特点有：

1. 深度为 $k$ 的完全二叉树，如果该树为满二叉树，则当前完全二叉树中结点最多。
2. 深度为 $k$ 的完全二叉树，如果第 $k$ 层，只有一个结点，则当前完全二叉树中结点最少。

二叉树的遍历

1. 前序遍历（先序遍历） 的遍历顺序为：根 $\to$ 左子树 $\to$ 右子树。
2. 中序遍历 的遍历顺序为：左子树 $\to$ 根 $\to$ 右子树。
3. 后序遍历 的遍历顺序为：左子树 $\to$ 右子树 $\to$ 根。

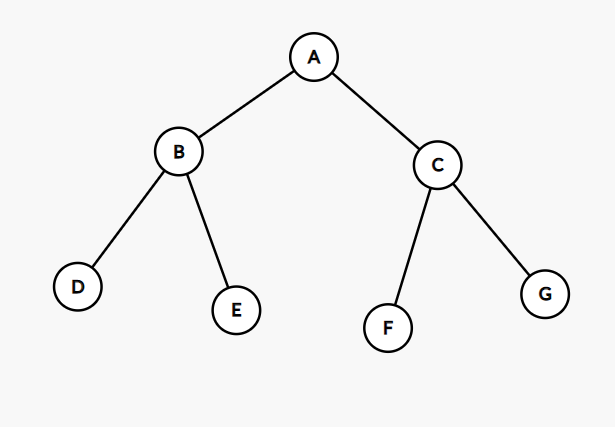
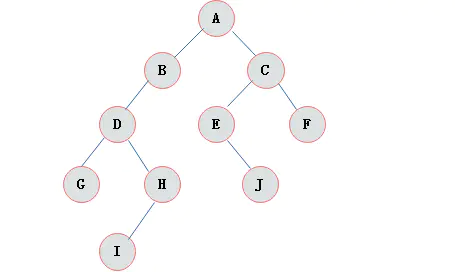
• 前序遍历序列：ABDECFG
• 中序遍历序列：DBEAFCG
• 前序遍历序列：DEBFGCA

前序遍历和中序遍历还原二叉树

1. 确定树的根节点，树根是当前树中所有元素在前序遍历中最先出现的元素。
2. 求解树的子树，找出根节点在中序遍历中的位置，根左边的所有元素就是左子树，根右边的所有元素就是右子树。若根节点左边或右边为空，则该方向子树为空，若根节点左边和右边都为空，则根节点已经为叶子节点。
3. 递归求解树，将左子树和右子树分别看成一棵二叉树，重复 1,2,3 步，直到所有的节点完成定位。

前序遍历和中序遍历还原二叉树

例如一颗二叉树的前序遍历为ABDECF，中序遍历为DBEAFC，我们现在来构造出一棵二叉树：

1. 整棵二叉树的根是A，因为前序遍历的第一个字符就是A。
2. 判断出A的左子树的中序遍历是DBE，右子树的中序遍历是FC。
3. 由于一棵树的中序遍历和先序遍历长度肯定是相同的，所以我们可以判断出A的左子树的先序遍历是BDE，右子树的先序遍历是CF。
4. 于是我们得到了两棵新的树，再对这两棵树分别按照刚才的方式继续构造即可。

最后的结果是：

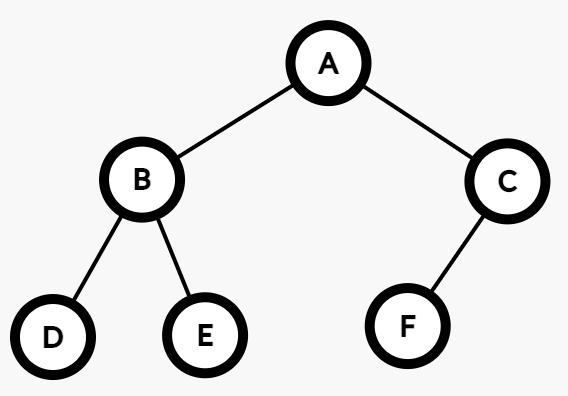
同理，后序遍历和中序遍历也可以还原唯一的二叉树。但是前序遍历和后序遍历不能还原唯一的二叉树。

排序二叉树

排序二叉树是一棵有顺序，且没有重复元素的二叉树。

对每个节点而言：

1. 如果左子树不为空，则左子树上的所有节点的权值都小于该节点的权值。
2. 如果右子树不为空，则右子树上的所有节点的权值都大于该节点的权值。

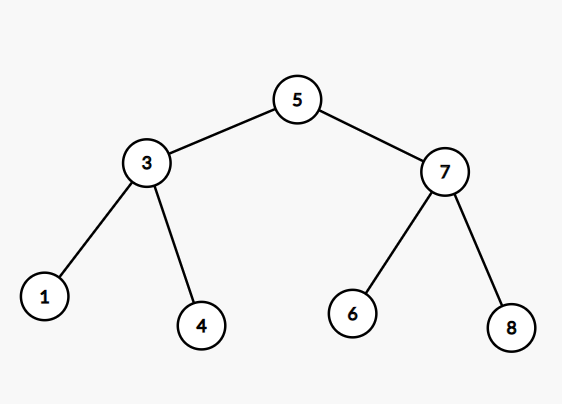
上图为一棵排序二叉树。相信你已经发现，将排序二叉树上的节点的权值按照中序遍历顺序排列成的序列，一定是严格单调递增的。

下面演示如何构造一棵排序二叉树，我们主要运用 DFS 的方法。

算法思想：

假定我们要将数值 $X$ 插入二叉树中。

1. 判断当前节点是否为空节点，若为空，则将 $X$ 插入到该节点处。
2. 若不为空，比较当前节点的权值与 $X$ 的大小。
3. $X$ 小于当前节点的值，进入当前节点的左子树。
4. $X$ 大于当前节点的值，进入当前节点的右子树。
5. 重复 $1,2,3,4$ 步。

一般树转为二叉树

对于二叉树而言，一个节点最多只有两个儿子，而且左右儿子分明，在处理一些树上问题的时候，二叉树会比普通树要方便得多。

所以也就有了将一般树转化为二叉树的算法。

这个算法很简单，我们针对树上的每一个节点 $x$ 和它的儿子们 $a1,a_2,\cdots, a_n$（按顺序排列的 $n$ 个儿子）进行重构，有：

1. $a_1$ 是 $x$ 的左儿子。

2. $a_2$ 是 $a_1$ 的右儿子。

3. $a_3$ 是 $a_2$ 的右儿子。

4. $\cdots$

5. $a_n$ 是 $a_{n-1}$ 的右儿子。

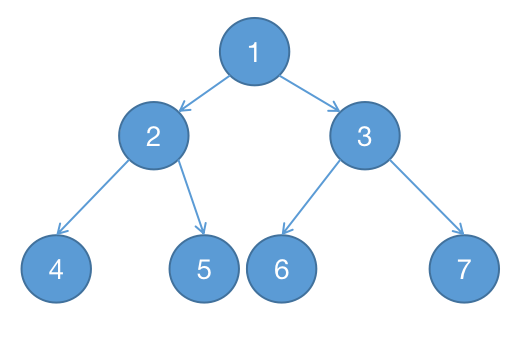
比如说下图的这棵根为 $1$ 的树：

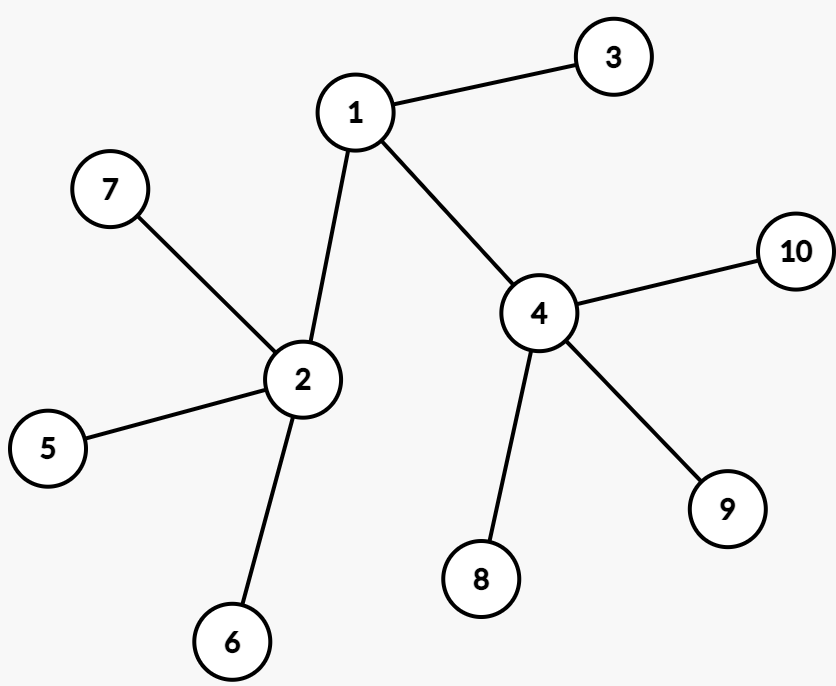
对于节点 $1$，在原树中它有三个儿子： $2,3,4$ ，我们就可以令在转换后的二叉树中：

1. $2$ 是 $1$ 的左儿子。
2. $3$ 是 $2$ 的右儿子。
3. $4$ 是 $3$ 的右儿子。

如果我们对原树中每一个节点的儿子们按照编号从小到大的顺序进行排列，在转换成二叉树之后会变成：

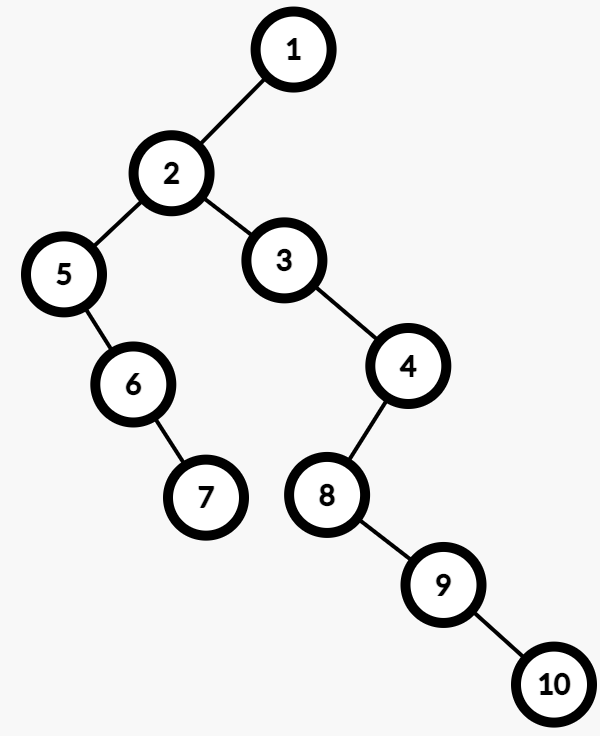
当然这并不是唯一解。假设你将每个节点的儿子们按照编号从大到小的顺序进行排列，就会出现另一种结果。但是反过来说，对于每一棵转换后的二叉树而言，原树是唯一的。

当然这个算法也是有缺点的，那就是树容易被退化成链，因为当一个节点的儿子太多的时候，树的深度会变得极大（例如下图）。

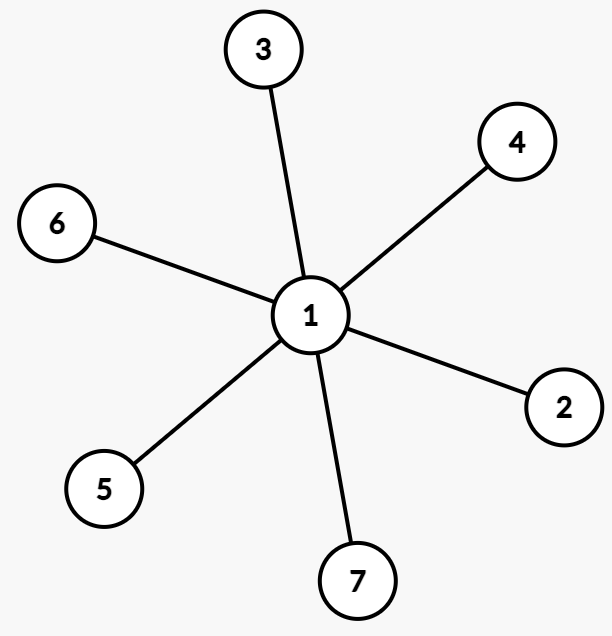
所以当相关算法的时间复杂度可能跟树的深度正相关时，这个算法就不适用了。

堆

堆是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。

堆总是满足下列性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一棵完全二叉树。

常见的堆有二叉堆、斐波那契堆等。

堆是非线性数据结构，相当于一维数组，有两个直接后继。

堆的定义如下：

$n$ 个元素的序列 ${k_{1},k_{2},\cdots,k_{i},\cdots,k_{n}}$，当且仅当满足下关系的其中之一时，称之为堆：

1. 对任意 $i = 1,2,3,4,\cdots,n/2$，满足 $k_{i}\le k_{2\times i},k_{i}\le k_{2\times i+1}$。
2. 对任意 $i = 1,2,3,4,\cdots,n/2$，满足 $k_{i}\ge k_{2\times i},k_{i}\ge k_{2\times i+1}$。

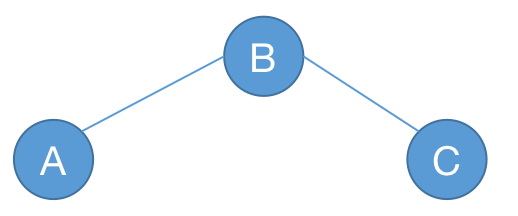
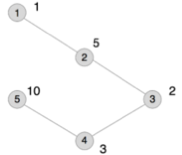
满足第一种条件时，我们称堆为小根堆；满足第二种条件时，我们称堆为大根堆。

左侧为小根堆，右侧为大根堆。

若将和此次序列对应的一维数组（即以一维数组作此序列的存储结构）看成是一个完全二叉树，则堆的含义表明，完全二叉树中所有非终端结点的值均不大于（或不小于）其左、右孩子结点的值。

由此，若序列 $k_{1},k_{2},\cdots,k_{n}$ 是堆，则堆顶元素（或完全二叉树的根）必为序列中n个元素的最小值（或最大值）。

下面我们来讲一下堆的插入、弹出操作（了解）。

向堆中插入一个新的元素时，其实就是在数组最末尾插入新的结点，然后开始自下而上的调整结点关系。时间复杂度：$\mathcal{O}(logn)$。

void push(int A[], int i, int &n) {
    n++; // 调整大小
    A[n] = i; // 放进堆的最后
    int p = n;
    while (p > 1 && A[p / 2] > A[p]) {// 调整，如果不满足堆的性质，交换父节点和当前节点。
        swap(A[p / 2], A[p]);
        p /= 2;
    }
}

删除堆顶元素，把堆存储的最后结点填在根节点处，再自上而下的调整结点关系。

时间复杂度：$\mathcal{O}(logn)$

void pop(int A[], int &n) {
    int res = A[1]; // 记录堆顶元素
    A[1] = A[n]; // 把最后一个元素替换到堆顶
    n--; // 调整大小，此时原来的最后一位虽然有值，但是不会在用了
    int p = 1, t;
    while (p * 2 <= n) { // 调整
        if (p * 2 + 1 > n || A[p * 2] <= A[p * 2 + 1]) { // 找到左右两个孩子中较小者
            t = p * 2;
        } else {
            t = p * 2 +1;
        }
        if (A[p] > A[t]) { // 如果不满足堆的性质就交换
            swap(A[p], A[t]);
            p = t;
        } else { //否则就调整完成了
            break;
        }
    }
}

优先队列

优先队列是一种常用的数据结构，多用于求解贪心类问题中。

优先队列与队列类似，但它是一种存在优先级的队列。

在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出的行为特征。

优先队列的头文件为#include<queue>，下面是优先队列的常用操作。

• empty() 如果队列为空，则返回真。
• pop() 删除堆顶元素。
• push(x) 向队列中加入一个元素 $x$。
• size() 返回优先队列中拥有的元素个数。
• top() 返回优先队列队头元素。

优先队列的声明：

priority_queue<int> q; //通过操作，按照元素从大到小的顺序出队。
priority_queue<int,vector<int>,less<int> >q;//通过操作，按照元素从大到小的顺序出队。
priority_queue<int,vector<int>, greater<int> > q; //通过操作，按照元素从小到大的顺序出队

其中，int类型可以改变成为其他的数据类型（自己声明的也可以）。

现在，我们来介绍一下，如何将我们自己定义的结构体变量加入到优先队列中。

这里，我们假设数据 int a 是判别数据优先级的标识。

struct node {
    int a,b;
    bool operator < (const node &x) const {
        return a < x.a;
    }
};

然后直接将node放入优先队列中即可。

priority_queue<node> q;
node x;
q.push(x);

映射二叉堆

定义

具有映射功能的堆称为双向映射堆。堆又名二叉堆，所以也常常称其为映射二叉堆。映射二叉堆相比普通的堆，核心功能是支持元素的快速查找，可以在 $\mathcal{O}(log$ $n)$ 的时间复杂度内找到索引为 $id$ 的元素（没有重复索引，索引并非堆中用来比较大小的关键字），并进行后续的修改或删除等操作。

映射二叉堆与普通堆的不同之处是它不存储数值，而是存储数据对应的索引。当需要比较父子结点的大小时，我们需要对两个索引对应的关键字进行比较；当需要交换父子结点时，我们要交换堆中父子结点的索引。在堆的外部还需要存储一个从索引到堆中元素的反向映射，用来在堆中检索指定索引的元素，进行后续的修改或删除操作。

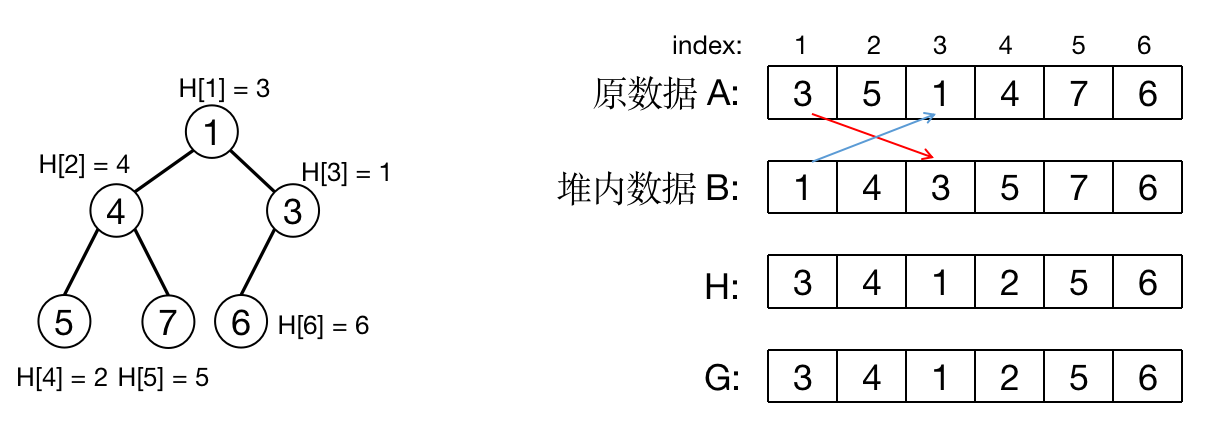
性质

映射堆元素内储存的索引本身是无序的，但它存放的索引对应的关键字是有序的，并且满足堆的性质。

存储堆的数组 $H[i] = j$ 表示 $H[i]$ 存放的是索引为 $j$ 的数据，反向映射 $G[j]=i$ 表示索引为 $j$ 的元素存储在 $H[i]$ 中，这样就可以实现映射二叉堆的双向映射。

通过 $H$ 数组，我们就可以迅速的查询到一个元素的位置，并对其进行删、改等操作。

常用操作的复杂度

插入

将插入的元素放在堆尾，自底向上调整（与父亲比较）。时间复杂度是 $\mathcal{O}(log$ $n)$。删除堆顶元素把堆顶元素与堆尾元素对调，调整堆容量，再自顶向下调整（与儿子比较）。

时间复杂度是 $\mathcal{O}(log$ $n)$ 。

删除

通过映射到堆的地址 $G[]$，找到指定索引在堆中存放的位置，然后将该位置与堆尾元素对调，再自底向上调整，或者自顶向下调整。在调整时我们不需要修改索引对应的关键字，只需分别交换 $H[]$ 和 $G[]$ 两个数组的值即可。

时间复杂度也是 $\mathcal{O}(log$ $n)$ 。

简易实现

我们可以用 STL 中的set来近似地实现映射二叉堆的功能。set内部是通过红黑树来实现的，而非堆，不过这并不妨碍我们用set来实现堆的功能。

堆的存储

我们可以用如下的结构来存储一个关键字为int类型堆：

#define PII pair<int, int>
set<PII, greater<PII> > gheap; // 定义了一个大根堆
set<PII, less<PII> > lheap; // 定义了一个小根堆
int keys[MAX_INDEX]; // 存储每个索引对应的关键字，如果索引的范围很大，可以用 map<int, int> 来储存

其中pair<int, int>的first储存关键字，second储存原始的索引（或下标）。接下来，我们都用大根堆来举例说明其他的用法。

堆的插入

使用如下的方法将关键字为value、索引为id的元素插入堆中。

gheap.insert(make_pair(value, id));  

获取及删除堆顶元素

我们可以在 $\mathcal{O}(log$ $n)$ 的时间复杂度内获取对应元素的关键字和索引。

set<PII, greater<PII> >::iterator iter = gheap.begin();
cout << iter->first << " " << iter->second << endl; // 第一个数是堆顶元素的关键字，第二个数是堆顶元素的索引

并在 $\mathcal{O}(log$ $n)$ 的时间复杂度内删除堆顶元素。

gheap.erase(*(gheap.begin()));

删除指定索引

我们可以在 $\mathcal{O}(log$ $n)$ 的时间复杂度内将堆中指定索引idx的元素删除。

gheap.erase(make_pair(keys[idx], idx));

远征

一辆卡车，初始时，距离终点 $L$ 距离，油量为 $P$，在起点到终点途中有 $n$ 个加油站，每个加油站油量有限，可以加 $a_{i}$ 的油量，而卡车的油箱容量无限，卡车在行车途中，每走一个单位的距离消耗一个单位的油量，给定 $n$ 个加油站距离终点的距离以及可以添加的油存储量。问卡车是否能到达终点，如果可达，最少需要加多少次油，否则不能到达，则输出 $-1$。

输入格式

第 $1$ 行：一个整数，$N(1\le N\le 10000)$。

第 $2\cdots N + 1$ 行：每行包含两个以空格分隔的整数，描述加油站：

第一个整数是从 目的地 到当前加油站的距离 $S(1\le S\le 10000000)$；

第二个是该站的可用燃料量 $W(1\le W\le 100)$。

第 $N + 2$ 行：两个以空格分隔的整数 $L$ 和 $P$。$(1\le L\le 10000000,1\le P\le 1000000)$

输出格式

一个整数，给出到达目的地所需最少加油的次数。如果无法到达目的地，则输出 $-1$。

输入样例

4
4 4
5 2
11 5
15 10
25 10

输出样例

2

采用贪心的思想，卡车当然在不加油的情况下走的越远越好了，而当它没油时，我们再判断卡车在途中经过的加油站，哪个加油站加的油最多，选油量最多的，这样后面加油次数也越少，然后又继续行驶，当它又没油了的时候，继续选它从起点到该点所经过的加油站油量最多的加油站中加油。

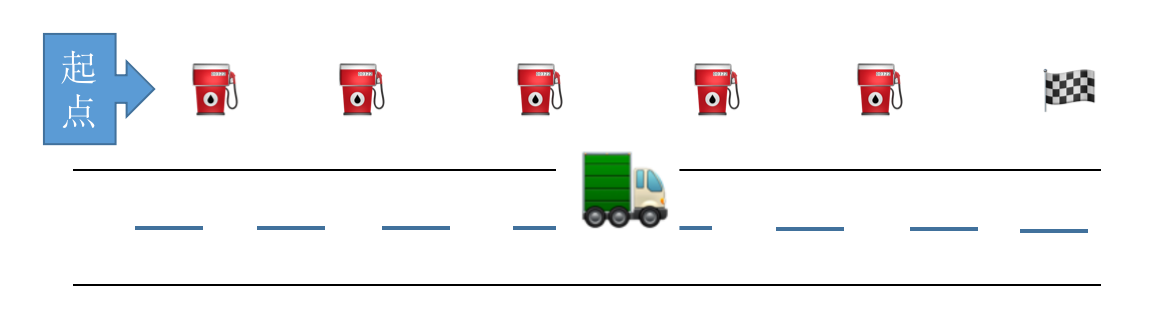
先将加油站到终点的距离由远到近排序，这样离起点就是由近到远。然后每经过一个加油站就将该加油站的油量压入优先队列中，然后每次没油的时候，去队首元素加油即可。

这里我们先创建一个struct结构体，用来存储加油站的信息。

struct node {
    int dis;    //加油站到起点的距离
    int fuel;   //加油量
    bool operator <（const node &x) const {
        return dis > x.dis;
    }
} stop[100005];

申请优先队列que

priority_queue<int> que; // 默认降序

接下来我们模拟刚刚讲过的算法过程，即：每经过一个加油站就将该加油站的油量压入优先队列中，然后每次没油的时候，去队首元素加油即可。

int l, p;        //l 表示距离目的地的距离，p 表示初始的油量。
int temp = 0;   //当前经过加油站的数量。
int ans = 0;    //最少需要加油的次数。
while (l > 0 && !que.empty()) {
    ans++;
    l -= que.top(); //加油，并且卡车能够行驶：que.top() 个单位的距离
    que.pop();
    while(l <= stop[temp].dis && temp < n)  //将经过的加油站压入优先队列中。
        que.push(stop[temp++].fuel);
}

当算法结束后进行判断，如果距离目的地的值 $l$ 大于 $0$ 说明无法到达目的地，否则说明可以到达，输出ans - 1。

if(l > 0) cout << "-1" << endl;  // l > 0说明到不了终点
else cout << ans - 1 << endl;  //减去 1 初始时油箱的油也被计算成一次加油了

维护中位数

初始序列为空，每次新加一个数，每加进一个数，都输出当前序列的中位数（如果序列长度为偶数，就输出中间两个数的平均值）。操作总共进行 $n$ 次。

$n\le 10^5$。

很明显，如果我们只开一个堆，是没有办法解决这个问题的。既然一个堆不够，我们就开两个堆。

我们现在需要找中位数，那么我们就需要让这个中位数处于堆顶，或者在两个堆之外。由此我们就想到了建堆的方式，令当前数列内有 $n$ 个数：

1. 建一个小根堆 $T1$，存储当前数列内最大的 $\lfloor \frac{n}{2} \rfloor$ 个数。
2. 建一个大根堆 $T2$，存储当前数列内最小的 $\lfloor \frac{n}{2} \rfloor$ 个数。

然后我们再开一个变量 $mid$，当 $n$ 为奇数时，表示数列的中位数。

那么当我们往数列内新加入一个数 $x$ 的时候，问题就变成了两种情况：

1). 当前长度 $n$ 为偶数（未加入 $x$ 时的长度）：

• 如果 $T1$ 的堆顶值比 $x$ 小，那么 $T1$ 的堆顶值便是新序列的中位数（mid = T1.top()），将它从 $T1$ 中弹出，并将 $x$ 加入 $T1$。
• 如果 $T2$ 的堆顶值比 $x$ 大，那么 $T2$ 的堆顶值便是新序列的中位数（mid = T2.top()），将它从 $T2$ 中弹出，并将 $x$ 加入 $T2$。
• 如果前面两个条件都不满足，那么 $x$ 便是新序列的中位数。

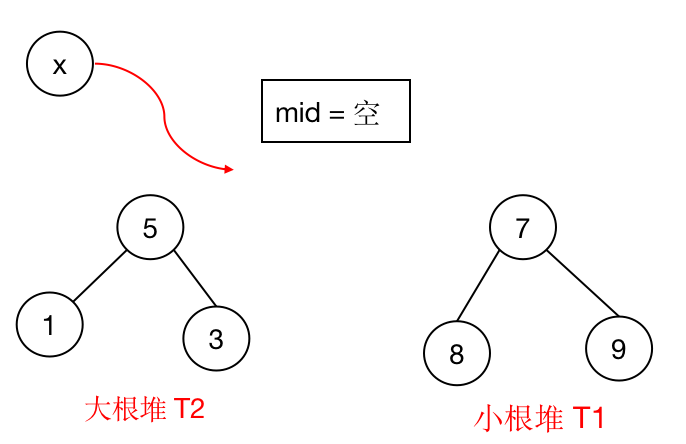
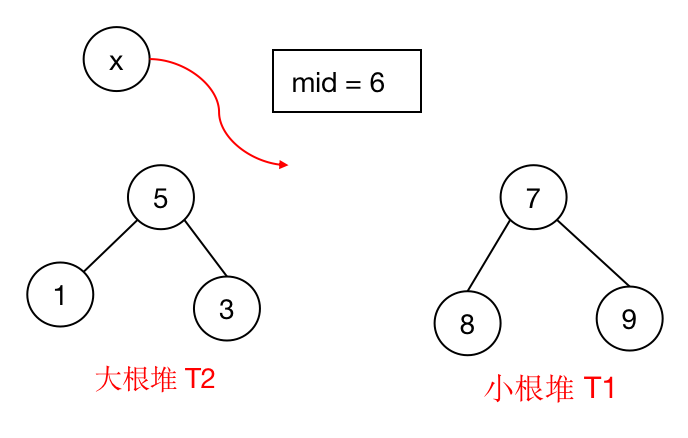
2). 当前长度 $n$ 为奇数（未加入 $x$ 时的长度）：这个就比较简单了，只需要比较 $x$ 与当前 $mid$ 的大小，将较小的那个放入 $T2$，较大的那个放入 $T1$，中位数为两个堆顶的平均值。

最短路

Floyd 算法

最短路：在一个图中在两结点之间寻找一条距离（边权和）最小的路。

当然，最短路也可以计算其他的度量，比如时间、花费等。

接下来介绍一种算法：Floyd 算法。该算法可以解决多源最短路问题，所谓多源则是它可以求出以每个点为起点到其它每个点的最短路。

概述

Floyd 算法是一种利用动态规划的思想、计算给定的带权图中任意两个顶点之间最短路径的算法。无权图可以直接把边权看作 $1$。

我们用 $dp_{k,i,j}$ 表示 $i$ 到 $j$ 能经过 $1\sim k$ 的点的最短路。那么实际上 $dp_{0,i,j}$ 就是原图，如果 $i,j$ 之间存在边，那么 $i,j$ 之间不经过任何点的最短路就是边长，否则，$i,j$ 之间的最短路为无穷大。

那么对于 $i,j$ 之间经过 $1\sim k$ 的最短路 $dp_{k,i,j}$ 可以通过经过 $1\sim k - 1$ 的最短路转移过来。

• 如果不经过第 $k$ 个点，那么就是 $dp_{k - 1,i,j}$。
• 如果经过第 $k$ 个点，那么就是 $dp_{k - 1,i,k} + dp_{k - 1,k,j}$。

所以就有转移$\displaystyle dp_{k,i,j} = min(dp_{k-1,i,j}, dp_{k-1,i,k} + dp_{k-1,k,j}) $

按照上面的动态规划的思想，我们可以写出下面的代码。

int g[N][N];  // 邻接矩阵存图
int dp[N][N][N];
void floyd(int n) {
    for (int k = 0; k <= n; k++) {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                if (k == 0) { // 初始化
                    dp[k][i][j] = g[i][j];
                } else { // 状态转移
                    dp[k][i][j] = min(dp[k - 1][i][j], dp[k - 1][i][k] + dp[k - 1][k][j]);
                }
            }
        }
    }
}

我们仔细分析，$dp_k$ 只能由 $dp_{k-1}$ 转移过来。并且 $dp_{k - 1,i,k} = dp_{k,i,k}$，因为 $i$ 到 $k$ 的最短路中间肯定不会经过 $k$。同理，$dp_{k - 1,k,j} = dp_{k,k,j}$。

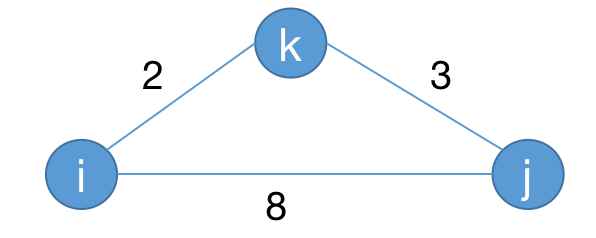
那么转移实际上变成了$\displaystyle dp_{k,i,j} = min(dp_{k-1,i,j}, dp_{k,i,k} + dp_{k,k,j}) $

这时候，我们尝试把 $k$ 这一维去掉，就用 $dp_{i,j}$ 来表示 $i, j$ 之间的最短路，那么转移变成了

$\displaystyle \forall{1 \le k \le n} \ \ \ dp_{i,j} = min(dp_{i,j}, dp_{i,k} + dp_{k,j}) $

这时候，$dp$ 数组就已经退化成为 $g$ 数组了。

我们写出最终的 Floyd 的形式，这也是常用的写法，优化了一维的空间。并且写法更加简单。如果理解了动态规划的思想，你就一定明白了为什么枚举的中间点 $k$ 一定要写在最外面。没有理解这一点，很容易把 $3$ 个循环的顺序弄错了。

刚才分析得出，最后的 $dp$ 数组退化成了 $g$ 数组，所以可以直接在原数组上操作。

int g[N][N];
void floyd(int n) {
    for (int k = 1; k <= n; k++) { // 中间点
        for (int i = 1; i <= n; i++) { // 起点
            for (int j = 1; j <= n; j++) { // 终点
                g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
            }
        }
    }
}

Floyd 算法本身的时间复杂度为 $\mathcal{O}(N ^ 3)$ ，邻接矩阵空间复杂度 $\mathcal{O}(N ^ 2)$ 在时间够用的情况下空间肯定也够用，并且邻接矩阵可以快速知道两个点之间是否相连。

这里在使用的时候因为邻接矩阵存的是距离，所以需要把不连通的部分赋值为一个很大的整数，避免其对答案产生影响，这样也可以根据这个无穷大判断两点间是否可达。

如果需要记录路径，可以记录一下每两个点之间最后是被哪个点更新的，然后一条路就可以被拆成两半不断递归找到路径了。

如果图中有负环的情况，Floyd 算法是求不出最短路的。此时会在不断在这个负环上转圈，所以负环上的点之间最短路为负无穷，这种情况下一般也只是判断出负环，不做其它处理，Floyd 算法无法判断这样的情况，所以就在没有负环的情况下使用，负环的判断在之后的算法中会给出方法。

Dijkstra 算法

单源最短路问题

单源最短路问题是指：求源点 $s$ 到图中其余各顶点的最短路径。

如果用 DFS 来解决单源最短路问题，效率上会很慢，能解决的问题的数据规模非常小。

而 BFS 能解决的最短路问题只限制在边权为 $1$ 的图上。对于边权不同的图，利用 BFS 求解最短路是错误的，比如下面这个图，如果用 bfs 解决，点 $3$ 和点 $4$ 的最短路求出来是错误的。

解决单源最短路径问题常用 Dijkstra 算法，用于计算一个顶点到其他所有顶点的最短路径。Dijkstra 算法的主要特点是以起点为中心，逐层向外扩展（这一点类似于 bfs，但是不同的是，bfs 每次扩展一个层，但是 Dijkstra 每次只会扩展一个点），每次都会取一个最近点继续扩展，直到取完所有点为止。

注意：Dijkstra 算法要求图中不能出现负权边。

算法流程

我们定义带权图 $G$ 所有顶点的集合为 $V$，接着我们再定义已确定从源点出发的最短路径的顶点集合为 $U$，初始集合 $U$ 为空，记从源点 $s$ 出发到每个顶点 $v$ 的距离为 $d_v$，初始 $d_s=0$。接着执行以下操作：

1. 从 $V-U$ 中找出一个距离源点最近的顶点 $v$，将 $v$ 加入集合 $U$。

2. 并用 $d_v$ 和顶点 $v$ 连出的边来更新和 $v$ 相邻的、不在集合 $U$ 中的顶点的 $d$，这一步称为松弛操作。

3. 重复步骤 1 和 2，直到 $V=U$ 或找不出一个从 $s$ 出发有路径到达的顶点，算法结束。

如果最后 $V \neq U$，说明有顶点无法从源点到达；否则每个 $d_i$ 表示从 $s$ 出发到顶点 $i$ 的最短距离。

Dijkstra 算法的时间复杂度为 $\mathcal{O}(V^2)$，其中 $V$ 表示顶点的数量。

算法演示

接下来，我们用一个例子来说明这个算法。

初始每个顶点的 $d$ 设置为无穷大 $\inf$，源点 $M$ 的 $d_M$ 设置为 $0$。当前 $U=\emptyset$，$V-U$ 中 $d$ 最小的顶点是 $M$。从顶点 $M$ 出发，更新相邻点的 $d$。

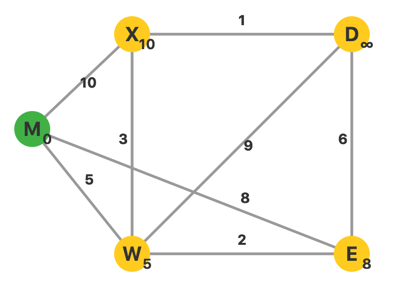
更新完毕，此时 $U={M}$，$V-U$ 中 $d$ 最小的顶点是 $W$。从 $W$ 出发，更新相邻点的 $d$。

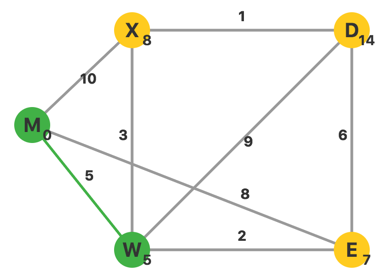
更新完毕，此时 $U={M,W}$，$V-U$ 中 $d$ 最小的顶点是 $E$。从 $E$ 出发，更新相邻顶点的 $d$。

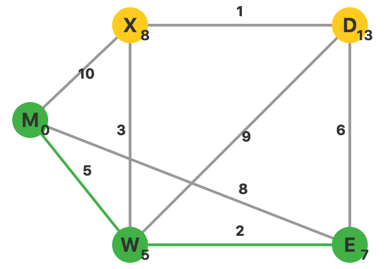
更新完毕，此时 $U={M, W, E}$，$V-U$ 中 $d$ 最小的顶点是 $X$。从 $X$ 出发，更新相邻顶点的 $d$。

更新完毕，此时 $U={M,W,E,X}$，$V-U$ 中 $d$ 最小的顶点是 $D$。从 $D$ 出发，没有其他不在集合 $U$ 中的顶点。

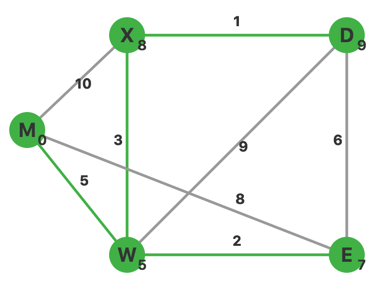
此时 $U=V$，算法结束，单源最短路计算完毕。

Dijkstra算法的优化

我们再回顾一下 的核心思想，就是一直维护一个还没有确定最短路的点的集合，然后每次从这个集合中选出一个最小的点去更新其他的点。

堆优化

如果每次暴力枚举选取距离最小的元素，则总的时间复杂度是 $\mathcal{O}(V^2)$。

结合之前学习的数据结构，如果考虑用堆优化，用一个 set 来维护点的集合，这样的时间复杂度就优化到了 $\mathcal{O}((V+E)\log V)$，对于稀疏图的优化效果非常好。

小根堆优化的 Dijkstra 示例代码如下：

set<pair<int, int> > min_heap;
min_heap.insert(make_pair(0, s));
while (min_heap.size()) {
    int v = min_heap.begin() -> second; // 取出最近的点
    min_heap.erase(min_heap.begin()); // 删除首元素
    for (int i = h[v]; i != -1; i = edge[i].next) {
        int to = edge[i].to;
        if (d[to] > d[v] + edge[i].len) {
            min_heap.erase(make_pair(d[to], to)); // 先删除原来的元素
            d[to] = d[v] + edge[i].len; // 更新距离
            min_heap.insert(make_pair(d[to], to)); // 加入新的元素
        }
    }
}

当然，既然是堆优化，我们也可以使用优先队列，具体的实现过程就不在此赘述了。

SPFA 算法

SPFA（Shortest Path Faster Algorithm）算法，在代码形式上接近于宽度优先搜索 BFS，是一个在实践中非常高效的 单源 最短路算法。

在 SPFA 算法中，使用 $d_i$ 表示从源点到顶点 $i$ 的最短路，额外用一个队列来保存即将进行拓展的顶点列表，并用 $in_queue_i$ 来标识顶点 $i$ 是不是在队列中。

1. 初始队列中仅包含源点，且源点 $s$ 的 $d_s=0$。
2. 取出队列头顶点 $u$，扫描从顶点 $u$ 出发的每条边，设每条边的另一端为 $v$，边 $<u,v>$ 权值为 $w$，若 $d_u+w<d_v$，则
   • 将 $d_v$ 修改为 $d_u+w$
   • 若 $v$ 不在队列中，则
     • 将 $v$ 入队
3. 重复步骤 $2$ 直到队列为空

最终 $d$ 数组就是从源点出发到每个顶点的最短路距离。如果一个顶点从没有入队，则说明没有从源点到该顶点的路径。

SPFA 思想

在一定程度上，也可以认为 SPFA 是由 BFS 的思想转化而来。从不含边权或者说边权为 $1$ 个单位长度的图上的 BFS，推广到带权图上，就得到了 SPFA。只是 BFS 能保证第一次访问就一定是最短路，而 SPFA 在每次更新了最短路以后又重新入队从而去更新后续结点的最短路。比如下图，$2$ 搜到 $3$ 的时候会再次更新 $3$ 最短路。

很显然，SPFA 的空间复杂度为 $\mathcal{O}(V)$。如果顶点的平均入队次数为 $k$，则 SPFA 的时间复杂度为 $\mathcal{O}(kE)$，对于较为随机的稀疏图，根据经验 $k$ 一般不超过 $4$。

示例代码

bool in_queue[MAX_N];
int d[MAX_N];  // 如果到顶点 i 的距离是 0x3f3f3f3f，则说明不存在源点到 i 的最短路
queue<int> q;
void spfa(int s) {
    memset(in_queue, 0, sizeof(in_queue));
    memset(d, 0x3f, sizeof(d));
    d[s] = 0;
    in_queue[s] = true; // 标记 s 入队
    q.push(s);
    while (!q.empty()) {
        int v = q.front();
        q.pop();
        in_queue[v] = false;
        for (int i = h[v]; i != -1; i = edge[i].next) {
            int to = edge[i].to;
            if (d[to] > d[v] + g[v][i].w) { // 更新
                d[to] = d[v] + g[v][i].w;
                if (!in_queue[to]) { // 如果之前没入队
                    q.push(to); // 入队
                    in_queue[to] = true; // 标记 to 入队
                }
            }
        }
    }
}

奶牛的比赛

FJ 的 $N(1\leq N\leq 100)$ 头奶牛们最近参加了场程序设计竞赛。在赛场上，奶牛们按 $1\cdots N$ 依次编号。每头奶牛的编程能力不尽相同，并且没有哪两头奶牛的水平不相上下，也就是说，奶牛们的编程能力有明确的排名。

整个比赛被分成了若干轮，每一轮是两头指定编号的奶牛的对决。如果编号为 $A$ 的奶牛的编程能力强于编号为 $B$ 的奶牛$(1\leq A\leq N; 1\leq B\leq N; A\neq B)$，那么她们的对决中，编号为 $A$ 的奶牛总是能胜出。

FJ 想知道奶牛们编程能力的具体排名，于是他找来了奶牛们所有 $M(1\leq M\leq 4,500)$ 轮比赛的结果，希望你能根据这些信息，推断出尽可能多的奶牛的编程能力排名。比赛结果保证不会自相矛盾。

$N\leq 100\ \rightarrow$ 条件反射 Floyd

注意到战胜的关系是传递的，一个奶牛的排名确定 $\leftrightarrow$ 这头牛和其他每一头牛的战胜关系都已知。

也就是我们要做的是，是通过已知信息，推断出所有的战胜关系，那么将 Floyd 稍微变形即可！

for(int k = 1; k <= n; k++){
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= n; j++){
            if(mark[i][k] == 1 && mark[k][j] == 1){
                mark[i][j] = 1;
            }
        }
    }
}

迷阵突围

STJ陷入了坐标系上的一个迷阵，迷阵上有 $n$ 个点，编号从 $1$ 到 $n$。STJ在编号为 $1$ 的位置，他想到编号为 $n$ 的位置上。STJ当然想尽快到达目的地，但是他觉得最短的路径可能有风险，所以他会选择第二短的路径。现在STJ知道了 $n$ 个点的坐标，以及哪些点之间是相连的，他想知道第二短的路径长度是多少。

注意，每条路径上不能重复经过同一个点；另外这里的第二短路指的是非严格次短路。

$1\leq n\leq 200$

这道题我们需要去求次短路的长度。我们令图 $G=(V,E)$。

首先我们肯定是要去求最短路长度的。那么在求得 $1$ 号点到其他点的最短路的时候，我们肯定也能够同时得到一条从 $1$ 号点到 $n$ 号点的最短路径。

那么，我们在更新最短距离的时候需要进行额外的标记，内容是到某个点的最短路径，最后一条边是从哪里出发过去的，我们可以开一个 pre 数组进行记录：

for (int j = h[v]; j != -1; j = edge[j].next) { // 更新最短距离
    if (d[to] > d[v] + edge[j].to) {
        d[to] = d[v] + edge[j].to
        pre[to] = v; // 代表当前到 g[v][j].v 的最短路的最后一条边是从 v 出发
    }
}

然后我们可以去把从 $1$ 到 $n$ 上的最短路的所有结点都取出来：

void getPath(int x) {
    if (x == 1) {
        return;
    }
    /*
    做点什么
    */
    getPath(pre[x]);
    /*
    你也可以在这里选择做点什么
    */
}

而在函数执行的途中，从 $pre_x$ 到 $x$ 的那条边便是 $1$ 到 $n$ 上的最短路径上的一条边。那么在主函数内，你只需要执行：

getPath(n);

就可以把 $1$ 到 $n$ 上的最短路的所有结点都取出来。

然后我们可以得到一个很显然的结论，在图 $G$ 上 $1$ 号点到 $n$ 号点的次短路肯定是 $G$ 的某个子图上 $1$ 号点到 $n$ 号点的最短路。于是我们现在就转变成了考虑在哪些子图上 $1$ 号点到 $n$ 号点的最短路可能会变成图 $G$ 上 $1$ 号点到 $n$ 号点的次短路。

而构造这些子图，我们很明显需要切断 $G$ 上 $1$ 号点到 $n$ 号点的最短路。而因为我们需要求的是次短路，所以删掉一条边就好。所以我们在图 $G$ 上得到一条从 $1$ 号点到 $n$ 号点的最短路径之后，枚举这条路径上的每一条边断掉，这样就可以形成一些子图，再对这些子图去做 $1$ 号点到 $n$ 号点的最短路，然后取最小值，便可以得到答案了。

而删除一条边，并不是真的需要去执行这个操作，你只需要在进行最短路算法的时候进行特判，当遇到这条被“删除”的边的时候不去处理就行了。

for (int j = h[v]; j != -1; j = edge[j].next) { // 更新最短距离
    int to = edge[j].to;
    if (x == v && y == to) { // 假设 x 到 y 的有向边是此次删除掉了的边
        continue;
    }
    if (d[to] > d[v] + edge[j].len) { //注意这里你不要再去更新 pre 标记了，因为 pre 标记记录的是图 G 的相关信息
        d[g[v][j].v] = d[v] + edge[j].len
    }
}

当然你需要注意的是，如果你删除的是一条 无向边，那么相当于删除了两条有向边，判断的时候需要千万小心。

香甜的黄油

农夫 John 发现做出全威斯康辛州最甜的黄油的方法：糖。把糖放在一片牧场上，他知道 $N(1\le N\le500)$ 只奶牛会过来舔它，这样就能做出能卖好价钱的超甜黄油。

农夫 John 很狡猾。他知道他可以训练这些奶牛，让它们在听到铃声时去一个特定的牧场。他打算将糖放在那里然后下午发出铃声，以至他可以在晚上挤奶。

农夫 John 知道每只奶牛都在各自喜欢的牧场（一个牧场不一定只有一头牛）。给出各头牛在的牧场和牧场间的路线，找出使所有牛到达的路程和最短的牧场，他将把糖放在那让牛去舔。

牧场间道路数 $C(1\le C\le 1450)$。

牧场数 $P(2\le P\le 800)$。

这道题实际上就是要求出所有有牛的牧场的到每个牧场的最短路。由于牧场的数量比较多，这里不能使用 floyd 算法了，所以可以考虑使用 $p$ 次 SPFA。

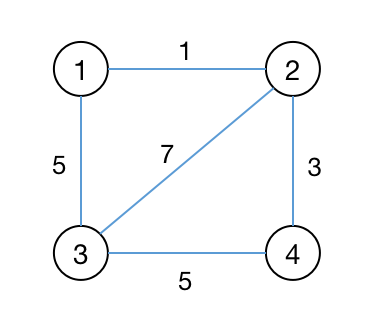
然后剩下的工作就是枚举每个牧场然后把每一头奶牛到这个牧场的最短路径长度加起来求个和，比较所有的和的最小值。

Nya Graph

Nya 图是一种有 $n$ 个点，由多个图层组成的无向图。每个点都属于一个图层。

第 $x$ 个图层的点和第 $x+1$ 个图层的点两两有边相连，且长度为 $c$。图上还有另外 $m$ 条边，每条边可以用整数元组 $(x,y,z)$ 表示，含义为 $x,y$ 之间还有一条长度为 $z$ 的无向边。

现在请问点 $1$ 到点 $n$ 的最短路长度是多少。

$0 \le n, m \le 10^5$

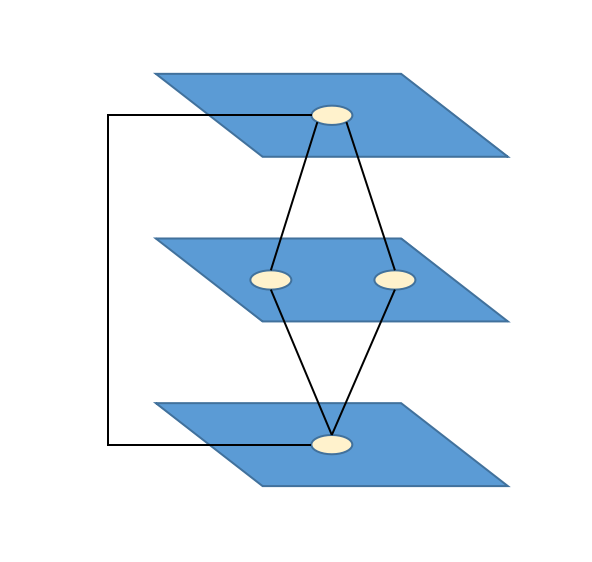
这道题很明显是不能直接按照题目里面的意思建图的。

比如说只有两个图层，每个图层有 $n/2$ 个点的时候，$n=10^5$，边的数量太多了，根本无法存储。

但是我们可以思考一下 第 $x$ 个图层的点和第 $x+1$ 个图层的点两两有边相连 实际上表达了两类点之间的连通性。

那么我们其实可以用 一个点 代替 一类点。

对于每一个图层，我们都生成一个新的点，用它们去代表一个图层，比如 $v_i$ 代表着第 $i$ 个图层。那么我们便可以让 $v_i$ 向所有属于第 $i$ 个图层的点都建立一条权值为 $0$ 的 有向边（为什么不是无向边你可以自己思考一下）。

然后所有属于第 $i$ 个图层的点向 $v_{i-1}$ 和 $v_{i+1}$ 分别建立一条权值为 $c$ 的 有向边。

至于还有另外的 $m$ 条边，这 $m$ 条边是不受影响的，该是 $x,y$ 之间有一条边连通还是这两个点之间有一条边。

这样子我们便将整个图的边的个数从 $O(n^2+m)$ 降低到 $O(n+m)$。这样我们便可以很好地存储这些边，并且直接在这个新的图上做最短路就可以完成这个问题。

迷阵突围（二）

STJ陷入了坐标系上的一个迷阵，迷阵上有 $n$ 个点，编号从 $1$ 到 $n$。STJ在编号为 $1$ 的位置，他想到编号为 $n$ 的位置上。STJ当然想尽快到达目的地，但是他觉得最短的路径可能有风险，所以他会选择第二短的路径。现在STJ知道了 $n$ 个点的坐标，以及哪些点之间是相连的，他想知道第二短的路径长度是多少。

$1\leq n\leq 200$

之前我们也讲过一道叫做迷阵突围的题，但是上节课的题目里面有这么一个条件：

每条路径上不能重复经过同一个点

而这道题里面没有。那么有没有这个条件到底会产生什么区别呢？举个例子：

$1 \sim 3$ 的最短路为 $1 \rightarrow 2 \rightarrow 3$，长度为 $2$。

每条路径上可以重复经过同一个点时，次短路为 $1 \rightarrow 2 \rightarrow 1 \rightarrow 2 \rightarrow 3$，长度为 $4$。

每条路径上不能重复经过同一个点时，次短路为 $1 \rightarrow 3$，长度为 $10$。

不能重复经过的情况上节课已经讲了，如果还不太清楚，可以去看看上节课的课件。

我们已经学习过 dijkstra 求最短路算法。那么我们这里也来尝试一下使用 dijkstra 求次短路。

在之前的算法中，我们寻找的是 未访问过的离起点距离最短 的点，将其取出并且向外扩展，但是这里我们还需要求次短路，很明显每个点取一次并不足够，因为没有办法在只取一次的情况下去把次短路算出来。

那么怎么办呢？一次不够，那就再来一次。再来一次，我们取的便是起点到一个点的次短路长度。

现在的问题就变成了怎么去保证第二次取到一个点的时候可以取到起点到该点的次短路。

这里我们直接讲使用堆优化的算法过程，并定义两个数组 $f1,f2$ 分别为起点到某个点的最短路和次短路长度。

首先需要将 $vis$ 数组的定义进行修改：现在变成了一个点我们已经取出来了几次。

1. 如果 $vis_i$ 现在为 $0$，那么下一次取出点 $i$ 的时候得到的应该是起点到 $i$ 的最短路。
2. 如果 $vis_i$ 现在为 $1$，那么下一次取出点 $i$ 的时候得到的应该是起点到 $i$ 的次短路。
3. 如果 $vis_i$ 现在为 $2$，那就说明我们已经得到了这个点的最短路和次短路，并且都已经扩展过了，不用再计算了。

然后在取用点 $i$ 的时候：

1. 如果取出的是起点到 $i$ 的最短路，那么我们就将 $(i,f1_i)$ 从堆中删除，将 $(i,f2_i)$ 加入堆。
2. 如果取出的是起点到 $i$ 的次短路，那么直接将 $(i,f2_i)$ 从堆中删除。

从起点 $1$ 到某个点 $y$ 的次短路径可以这么表示：$1\rightarrow x\rightarrow y$，我们并不能，也没有必要去考虑 $1\rightarrow x$ 的这条路径是最短路的还是次短路（因为都有可能）。所以我们并不需要在加入堆的数据中特地去标注该条信息是最短路还是次短路。

最后是进行扩展的时候，这个就简单了，我们在扩展的时候同时对最短路和次短路进行更新即可。

算法有些复杂，我们可以借助代码进行理解：

for (int i = 1; i <= 2 * n; i++) {
    int dis = T.begin() -> first;
    int v = T.begin() -> second;
    T.erase(T.begin());
    if (vis[v] == 0) {
        T.insert(make_pair(f2[v], v));
    }
    vis[v]++;
    for (int j = h[v]; j; j = a[j].next) {
        to = a[j].to;
        if (f1[to] > dis + a[j].len) { // 更新最短路
            f2[to] = f1[to]; // 更新次短路
            // 修改 set 内部数据，先删后改
            T.erase(make_pair(f1[to], to)); 
            f1[to] = dis + a[j].len;
            T.insert(make_pair(f1[to], to));
        } else if (f2[to] > dis + a[j].len) { 
            //不能更新最短路，但是可以更新次短路
            // 如果存在次短路，那么对 set 内部的数据进行修改
            if (vis[to] == 1) {
                T.erase(make_pair(f2[to], to));
            }
            f2[to] = dis + a[j].len;
            if (vis[to] == 1) {
                T.insert(make_pair(f2[to], to));
            }
        }
    }
}

初始化代码也提供一下，加深同学们对上面代码的理解：

for (int i = 1; i <= n; i++) {
    f1[i] = inf;
    f2[i] = inf;
}
f1[1] = 0;
T.insert(make_pair(0, 1));

并查集

并查集

并查集实际上是三个词的简称：合并，查询，集合。

实际上这三个词便反映了两种操作：

1. 集合的合并。
2. 集合的查询。

当然，这些集合本身是 互不相交 的。

如果我们用形式化的定义这两种操作，是这样的：

1. 合并元素 $x$ 所在的集合和元素 $y$ 所在的集合，当然如果已经在一个集合了，就什么都不做。
2. 查询元素 $x,y$ 现在是否在一个集合里。

那么作为一种数据结构，并查集的数据便是一个又一个的集合。初始状态下，一个集合里面一般只有一个元素，比如说，第 $i$ 个集合里面只有元素 $i$。

我们可以将上面的操作转换成一个图论模型，图里面有 $n$ 个点，但是没有边。

然后我们来把两种操作转换到图上。

1. 合并元素 $x$ 所在的集合和元素 $y$ 所在的集合：把点 $x,y$ 之间连一条无向边，这就表示 $x,y$ 在同一个集合里了。

2. 查询元素 $x,y$ 现在是否在一个集合里：求问 $x,y$ 之间是否有一条路径相连。

这个模型最大的问题在于，寻找 $x,y$ 之间是否有一条路径相连会是一件效率很低的事。

那么我们来想一想，我们至始至终都只是询问 是否有路径，而不是求具体的路径或求 有几条路径。

所以我们只需要存在一条路径即可。而一个无向连通块内任意两点都有且只有一条路径，这样的图我们称为 树。问题便由 是否存在路径 变成了 是否在同一棵树 里，而在同一棵树里面的两个点，如果对它们分别求解所在树的根，必然会得到相同的结果。

由此，我们再修改一下这两种操作：

1. 合并元素 $x$ 所在的集合和元素 $y$ 所在的集合：先查询元素 $x,y$ 现在是否在一个集合里，如果不在，那么分别找到 $x,y$ 所在的集合树的根 $x_1,y_1$，并将 $y_1$ 的父亲设为 $x_1$。

2. 查询元素 $x,y$ 现在是否在一个集合里：求问 $x,y$ 所在的集合树的根是否是一样的，如果是一样的，那么就在同一个集合里；如果不一样，那么就不在一个集合里。

如下图：

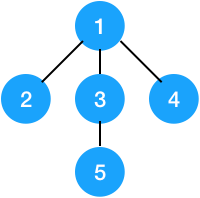
记录每个节点的父亲的数组fa中是这样的：

fa[1] = 1; fa[2] = 1; fa[3] = 1; fa[4] = 1; fa[5] = 3;

根节点的fa值为它自己，其它点的fa值为该点直接的父节点。

并查集可以维护无向图连通块，同属于一个集合的点互相连通，并且可以用集合树的 根节点 表示这个连通块。

有向图连通要求必须按照有向图边的方向走，那么并查集就无法维护了。在之后的阶段我们会学习关于有向图和无向图更多的连通性相关的问题。

如果这个连通块的根为u，就可以把一些连通块的信息放在一些数组下标为u的位置了。

初始化：初始的时候每个节点各自为一个集合，$fa[i]$ 表示节点 $i$ 的父亲节点，如果 $fa[i] = i$，我们认为这个节点是当前集合根节点。

void init() {
    for (int i = 1; i <= n; i++) {
        fa[i] = i;
    }
}

查找：查找节点所在集合的根节点，节点 $x$ 的根节点必然也是其父亲节点的根节点。

int get(int x) {
    if (fa[x] == x) { // x 节点就是根节点
        return x;
    }
    return get(fa[x]); // 返回父节点的根节点
}

合并：将两个元素所在的集合合并在一起，实际上就是把两个元素的根节点进行合并。通常来说，合并之前先判断两个元素是否属于同一集合。

void merge(int x, int y) {
    x = get(x);
    y = get(y);
    if (x != y) { // 不在同一个集合
        fa[y] = x;
    }
}

如果只是合并，其实也可以不判断x != y，因为x == y的时候这样操作也没事，但是我们经常在合并不在同一集合中的两个点的时候改变一些其它的信息，比如合并 $x$ 和 $y$ 有一定的代价，那就需要加上这个代价，这个时候就需要先判断一下 $x$ 和 $y$ 在不在同一集合了。

一定注意合并的是两个根节点，因为我们只记录了每个节点的直接父节点，所以如果不是合并根节点可能会丢一些信息。

如下图：

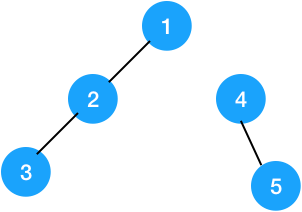
如果这一次合并的是 $2$ 和 $5$，如果把 $fa_2$ 改了，那节点 $1$ 就不在集合里了，如果把 $fa_5$ 改了，那节点 $4$ 就不在集合里了，所以我们找到两个集合的根 $1$ 和 $4$ 这样连，保证这个集合一个点都没丢。

并查集的路径压缩

我们已经学习了并查集最核心的操作。

但是接下来我们再来看这么一组数据（只有合并操作）：

2 1
3 1
4 1
5 1
6 1
7 1
8 1
...

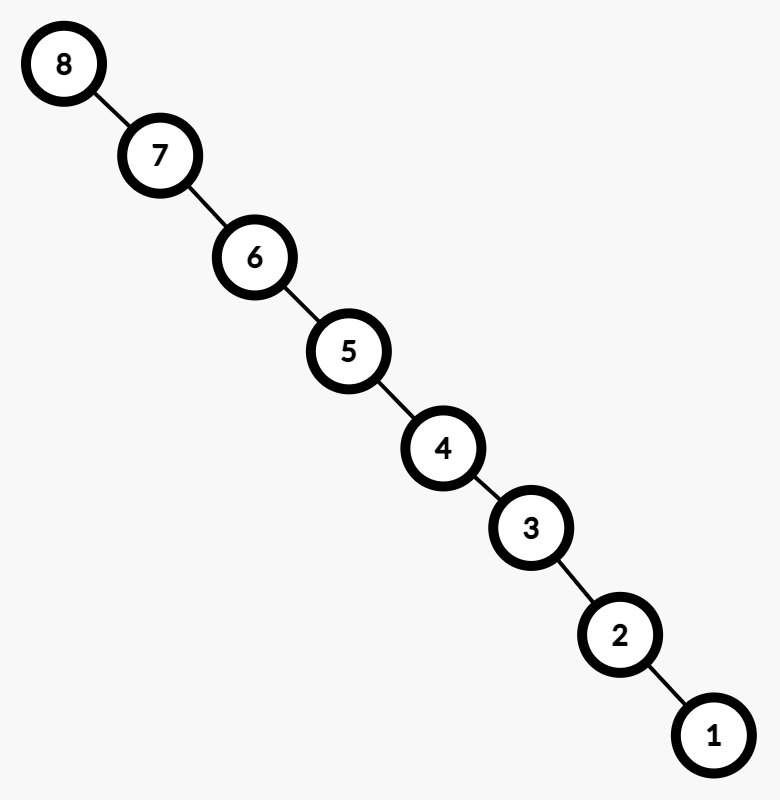
我们会发现集合树退化成了一条链。这样对于一个节点去寻找它所在的集合树的根，复杂度可能会达到 $O(n)$。

于是我们又注意到：我们只需要解决 根是什么 的问题，而并不需要去关注 结点到根上的路径 的问题。所以我们对于路径本身和之前的路径个数一样，也需要进行简化。

比如说对于给出的图例，我们要求 $1$ 所在的集合树的根，那么我们会得到 $1$ 到 $8$ 的路径：

\[1→ 2→ 3→ 4→ 5→ 6→ 7→ 8\]

我们可以得到 $1$ 所在的集合树的根是 $8$，并且 $2,3,4,5,6,7$ 所在的集合树的根也是 $8$。

由此我们可以直接把路径上所有的点的父亲直接指向集合树的根：

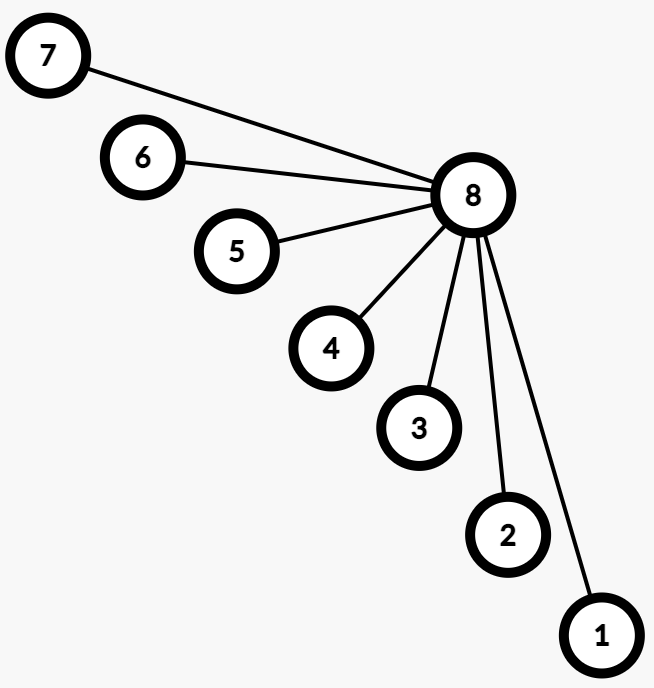
那么路径压缩的实现也很简单，我们把寻找根的函数做简单修改即可：

int get(int x) {
    if (fa[x] == x) {
        return fa[x];
    }
    //return get(fa[x]); 这是修改前的操作

    fa[x] = get(fa[x]); //路径压缩
    return fa[x];
}

算法的时间复杂度是 $O(m\log n)$，其中 $m$ 是执行合并操作的次数。

网络社交

在网络社交的过程中，通过朋友，也能认识新的朋友。在某个朋友关系图中，假定 A 和 B 是朋友，B 和 C 是朋友，那么 A 和 C 也会成为朋友。即，我们规定朋友的朋友也是朋友。

现在要求你每当有一对新的朋友认识的时候，你需要计算两人的朋友圈合并以后的大小。

输入格式

第一行：一个整数 $n(1 \leq n\leq 50000)$，表示有 $n$ 对朋友认识。

接下来 $n$ 行：每行输入两个名字。表示新认识的两人的名字，用空格隔开。（名字是一个首字母大写后面全是小写字母且长度不超过 $20$ 的串）。

这道题实际上有两个难点：

1. 名字是字符串，怎么处理？
2. 怎么统计合并以后的朋友圈大小。

还记得 映射表 吗？实际上我们可以将这最多 $2\times n$ 个不同的名字映射为从 $1$ 开始的若干个正整数。

那么这个问题便得以解决了，接下来解决第二个问题。

之前中我们已经讲过，我们可以用集合树的根来表示整个集合，自然可以用一个数组去存储以一个某个点为根的集合的大小。令这个数组叫 $num$，那么在合并两个集合的时候：

void merge(int x, int y) {
    x = get(x);
    y = get(y);
    if (x != y) {
        fa[y] = x;
        num[x] += num[y]; //统计合并后集合的大小
    }
    cout << num[x] << endl; //输出集合的大小
}

关押罪犯

$S$ 城现有两座监狱，一共关押着 $N$ 名罪犯，编号分别为 $1 \sim N$ 。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久，如果客观条件具备则随时可能爆发冲突。我们用“怨气值”（一个正整数值）来表示某两名罪犯之间的仇恨程度，怨气值越大，则这两名罪犯之间的积怨越多。如果两名怨气值为 $c$ 的罪犯被关押在同一监狱，他们俩之间会发生摩擦，并造成影响力为 $c$ 的冲突事件。

每年年末，警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表，然后上报到 $S$ 城 $Z$ 市长那里。公务繁忙的 $Z$ 市长只会去看列表中的第一个事件的影响力，如果影响很坏，他就会考虑撤换警察局长。

在详细考察了 $N$ 名罪犯间的矛盾关系后，警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配，以求产生的冲突事件影响力都较小，从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨，那么他们一定会在每年的某个时候发生摩擦。那么，应如何分配罪犯，才能使 $Z$ 市长看到的那个冲突事件的影响力最小？这个最小值是多少？

对于 $100\%$ 的数据有 $N \le 20000$，$M \le 100000$。

希望你思考一下，然后翻到下一页。

很明显，我们要先安排怨气值最大的罪犯到不同的监狱里面，直到遇到一对罪犯它们必须在同一个监狱，那么他们将发生冲突并且造成一定影响力。

那么这道题的难点实际上在于怎么去定义集合本身。对于现在需要处理的一对罪犯 $x,y$ 如果他俩不必须在同一个监狱中，那么有：

1. $x$ 应该属于 不能和罪犯 $y$ 在同一个监狱的罪犯 的集合。
2. $y$ 应该属于 不能和罪犯 $x$ 在同一个监狱的罪犯 的集合。

例如分别加入数据：$1,2$ 不能在一个监狱内；$2,3$ 不能在一个监狱内；

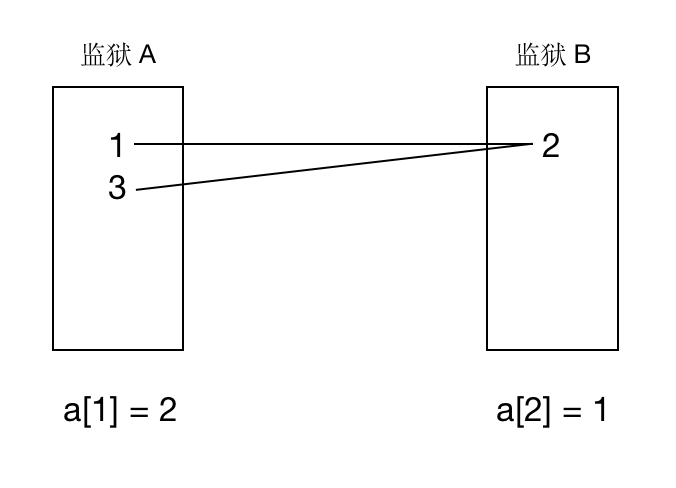
所以我们可以定义一个数组 $a$，$a_i$ 表示不能和罪犯 $i$ 在同一个监狱的罪犯的集合。如果这个集合现在还是空的，那么 $a_i=0$，否则代表的是这个集合内的一个元素。

所以当处理 $x,y$ 这一对犯人的时候，我们分以下步骤：

1. 若 $a_y=0$，则 $a_y=x$。
2. 否则将 $x$ 加入到 $a_y$ 所在的集合中。
3. 若 $a_x=0$，则 $a_x=y$。
4. 否则将 $y$ 加入到 $a_x$ 所在的集合中。

然后从怨气值最大的那对罪犯依次往下处理，直到遇到一对罪犯他们已经在一个集合中为止。>

树上基础算法

最小生成树

有 $n$ 座基站，你要在基站之间布设光纤，使得任意两座基站都是连通的，光纤传输具有传递性，即如果基站 $A$ 和基站 $B$ 之间有光纤，基站 $B$ 和基站 $C$ 之间有光纤，则基站 $A$ 和基站 $C$ 也是连通的，可以通过中间基站 $B$ 来完成传输。

不同的基站之间布设光纤的费用是不同的，现在你知道了任意两座基站之间布设光纤的费用，求问如何布设，可以使得任意两座基站都是连通的，且总费用最小。

生成树

为了解决这个问题，我们在这里引入一个名为生成树的概念。

在图论中，无向图 $G$ 的 生成树 是具有 $G$ 的全部顶点，但边数最少的连通子图。

更通俗地来说，有 $n$ 个顶点的无向连通图 $G$ 的生成树就是：在这张图中选择 $n-1$ 条边，将整个图连通。 $n$ 个顶点和选择的 $n-1$ 条无向边所构成的树就是 生成树。

所以我们发现，实际上我们布设光纤时，就需要使其最终形态是原图的生成树，这样才可以连通所有的基站。

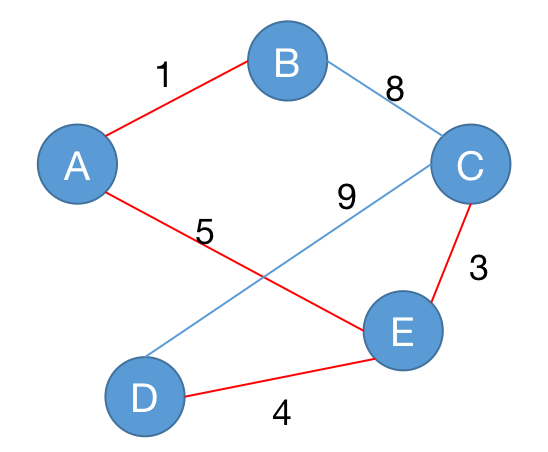
原图:

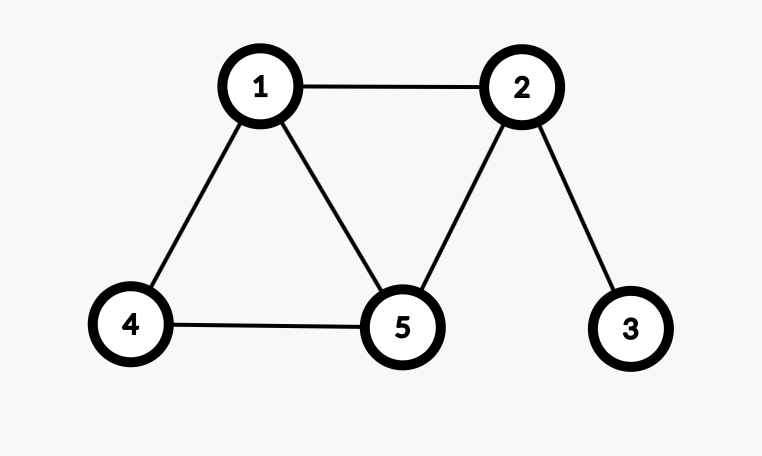
第一种生成树:

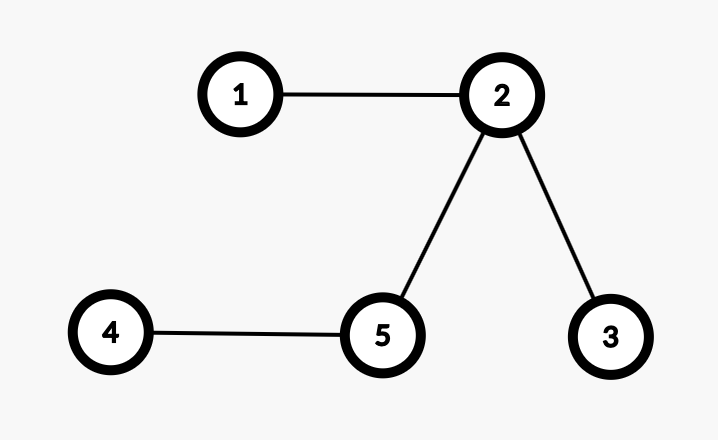
第二种生成树:

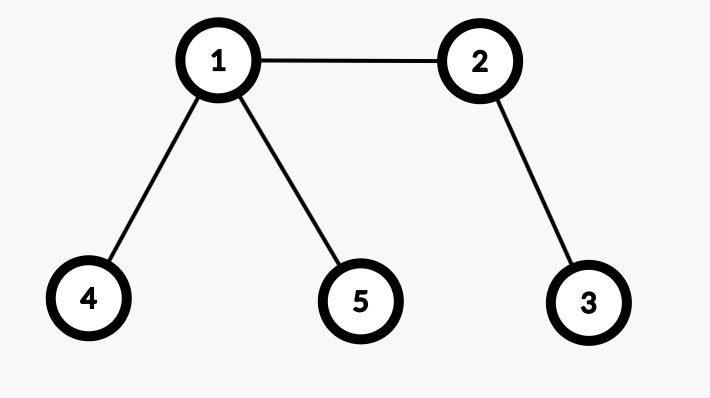
最小生成树

题目中不仅要求了所有基站之间连通，还要求总费用最小。所以我们引入这次主要学习的概念：最小生成树

在无向带权连通图 $G$ 中，有 $n$ 个顶点，每条边都有边权。这个图的所有的生成树当中，边权和最小的生成树就叫做最小生成树 (Minimum Spanning Tree)。

Kruskal 算法

Kruskal 算法是一种常见且简单的最小生成树算法，由 Kruskal 发明。该算法的核心思想是：按照边权从小到大将原图的边加入到生成树中，本质是个贪心算法。

思路很简单，为了生成最小生成树，Kruskal 算法从边权最小的边开始，按边权从小到大依次枚举每一条边并尝试将这条边加入到当前的生成树中，如果这次加边不会产生环，就加入这条边。直到加入了 $n-1$ 条边，即形成了一棵树时，算法运行结束。

此时问题就来到了如何判断是否产生环。

实际上我们发现，往生成树里面加入第一条边之前，我们可以将这 $n$ 个点看作是 $n$ 棵树，每一次加入边的时候都是把两棵树合并起来。在这样的情况下，如果有一条边连接的是已经在一棵树里面的点，就会形成环。

而我们刚刚学习过的并查集就可以很完美的解决这个问题。

这里我们来举个例：有这样一张图，图上有 $5$ 个顶点和 $7$ 条边。

第一步：将所有的边按边权从小到大排序。排序完成后，我们选择权值最小的边 $\lt J, N\gt$。这样我们的图就变成了：

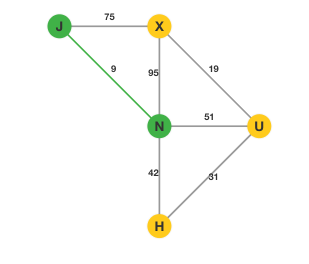
第二步，在剩下的边中寻找权值最小的边 $\lt U, X\gt$：

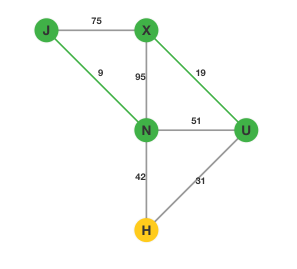
依次类推我们找到 $\lt H, U\gt$，图变成：

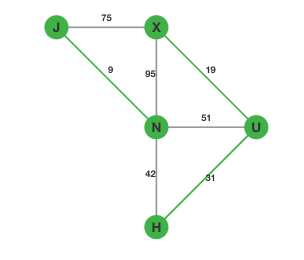
最后我们只需要再选择 $\lt H, N\gt$：

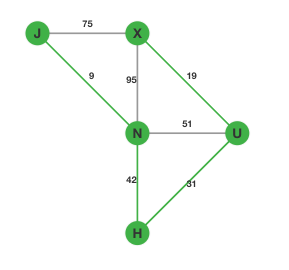
至此所有的点都已经连通，一个最小生成树构建完成。

Kruskal 算法的时间复杂度由主要排序算法决定。对于一个有 $n$ 个顶点和 $m$ 条边的无向图，Kruskal 算法的时间复杂度为 $\mathcal{O}(m\log m+m\times \alpha(n))$，鉴于上节课我们已经讲过可以将 $\alpha(n)$ 当作一个常数，所以时间复杂度为 $\mathcal{O}(m\log m)$ 。

证明 Kruskal

接下来我们用归纳法证明算法的正确性：

在 Kruskal 算法第一次加入边之前，所维护的生成树是空图，显然空图是最小生成树的子图。

假设 Kruskal 算法运行过程中，维护的生成树是某个最小生成树 $T$ 的子图，并且接下来要将边 $e$ 加入到算法所维护的生成树中。如果 $e \in E(T)$，那么我们维护的生成树在加入这条边后依然是最小生成树 $T$ 的子图。

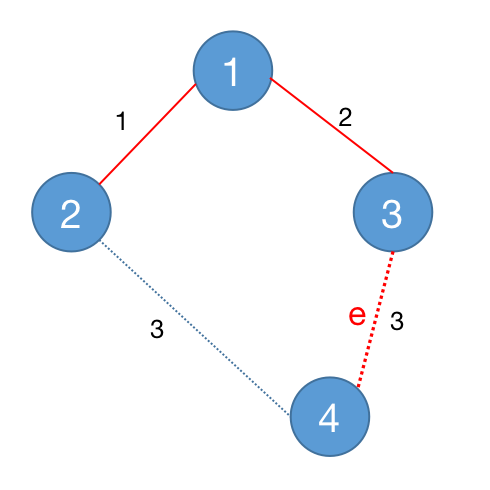
否则, 我们考虑将 $e$ 这条边加入到 $T$ 中。可以发现，加入了 $e$ 的图 $T$ 一定会形成一个环，并且这个环中一定存在一条不为 $e$ 的边 $f$， 而且这条边 $f$ 在之前的枚举边的过程中没有被枚举过。

我们发现:

• $f$ 的权值不会小于 $e$ ，否则该边会在枚举到 $e$ 之前被枚举到。
• $f$ 的权值不会大于 $e$ ，否则 $T’ = (V,E-f+e)$ 是一颗边权和比最小生成树 $T$ 的边权和更小的生成树。这就不满足 $T$ 是最小生成树的定义。

所以 $f$ 的权值一定等于 $e$

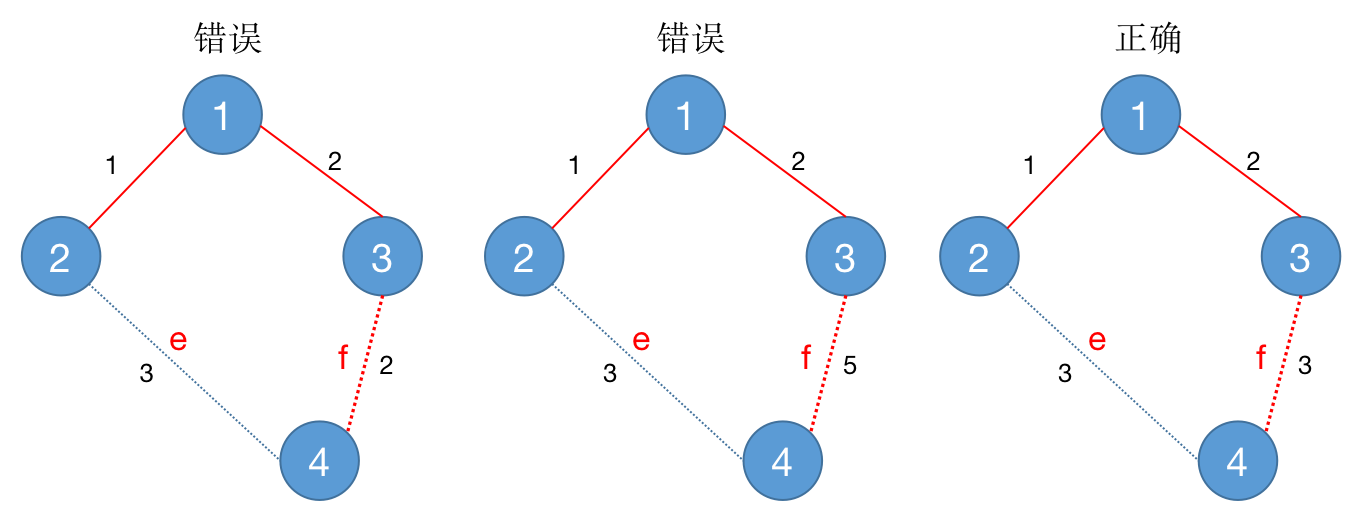
所以，此时新加入边 $e$ 后生成的生成树是最小生成树 $T’ = (V,E-f+e)$ 的子图

通过归纳法，每一次 Kruskal 算法加入一条新边后都满足当前维护的生成树是某一个最小生成树的子图。所以当维护的生成树的边为 $n-1$ 条时，这个生成树就是最小生成树。

Prim 算法

我们刚才学习了 Kruskal 算法，一般求解最小生成树都会使用 Kruskal 算法，因为非常简便。

而求解最小生成树的算法不止一种，多了解一些算法有助于拓展我们的思维，所以接下来我们了解一下 Prim 算法。

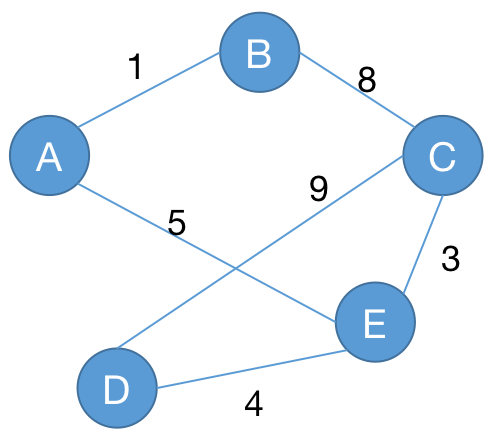
Prim 算法与 Dijkstra 算法类似，我们维护一个当前选择的点的集合，表示我们当前的生成树中有这些点。

接下来，每次找到距离当前点集最近的一个顶点，将这个顶点加入到当前点集中，并且将这个顶点与点集相连的边加入到生成树中。

核心代码

#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int maxn = 1001;
const int maxm = 10101;
const int inf = 0x3f3f3f3f;
struct Edge {
    int to, next, len;
} edge[maxm * 2];
int h[maxn], tot = -1;
int n, m, s;
int d[maxn];
bool vis[maxn];
void addEdge(int x, int y, int len) {
    edge[++tot] = (Edge) {y, h[x], len};
    h[x] = tot;
}
int prim() {
    memset(d, 0x3f, sizeof(d));
    d[s] = 0;
    int sum = 0;
    for (int i = 1; i <= n; i++) {
        int mind = inf;
        int v = 0;
        for (int j = 1; j <= n; j++) {
            if (!vis[j] && d[j] < mind) {
                mind = d[j];
                v = j;
            }
        }
        if (mind == inf) {
            break;
        }
        vis[v] = true;
        sum += d[v];
        for (int j = h[v]; j != -1; j = edge[j].next) {
            int to = edge[j].to;
            d[to] = min(d[to], edge[j].len);
        }
    }
    return sum;
}
int main() {
    cin >> n >> m >> s;
    memset(h, -1, sizeof(h));
    for (int i = 0; i < m; i++) {
        int u, v, w;
        cin >> u >> v >> w;
        addEdge(u, v, w);
        addEdge(v, u, w);
    }
    cout << prim() << endl;
    return 0;
}

当所维护的点集大小为 $n$ 时，此时的生成树就是最小生成树。

这个算法的时间复杂度取决于如何找到距离当前点集最近的点，我们可以使用二叉堆来完成这个过程，时间复杂度为：$\mathcal{O}((n+m)\log m)$。

最小生成树性质

在一个 $n$ 个顶点， $m$ 条边的无向边带权的连通图中，现在要删除一些边使得这个图中不存在环，并且使得所删除的边的权值和最大。求这个最大的权值和。

使这个图中没有环，也就是说删边过后整个图是一颗树。容易发现按照题目要求，最后保留下来的边构成了原图的最小生成树，所以可以直接用所有边的权值和减去最小生成树的权值和。

树的边权和 = 全部边的权值和 - 删除的边的权值和

即：删除的边的权值和 = 全部边的权值和 - 树的边权和

想要「删除的边的权值和」最大，那么「树的边权和」应该最小，故此树应该为最小生成树。

求一个无向边带权连通图的生成树，使这个生成树的最大边权最小。

容易发现，按照 Kruskal 算法的求解过程，每一次都会尽量尝试加入边权更小的边。

所以我们可以发现：最小生成树就是最大边权最小的生成树。

求一个无向边带权连通图的最大生成树

可以简单地将 Kruskal 算法中按照边权从小到大排序改为从大到小排序，剩余的部分不用改变。

由 Kruskal 算法正确性的证明可以得知，改变边的排序方式后求出的就是最大生成树。

树的重心

树的重心是树的某一个点，使得当整颗树以这个点为根时，根节点的所有子树中最大的子树结点数最小。树的重心可以使得我们删除这个重心时，生成的多棵树中结点个数尽量均衡。

我们首先假定树的根结点为 $1$ ，然后我们可以用一次 DFS 搜索求出以每个结点为根的子树的大小。

假设以结点 $u$ 为根的子树大小用 $\text{siz}_u$ 表示。我们现在考虑计算当结点 $u$ 为整颗树的根时，它的所有子树中最大的子树的结点数。

我们首先需要统计它的所有子树的 $\text{siz}$ ，因为这是在以 $1$ 为根的前提下计算的，所以结点 $u$ 此时的父亲结点所在的上半部分实际上也需要当作它的子树进行计算，这棵“子树”的结点个数可以用 $\text{总结点数}-\text{siz}_u$ 来计算得到。

\[\displaystyle f_u = max\{max_{v\text{ is child of }u}\{\text{siz}_v\},n-\text{siz}_u\}\]

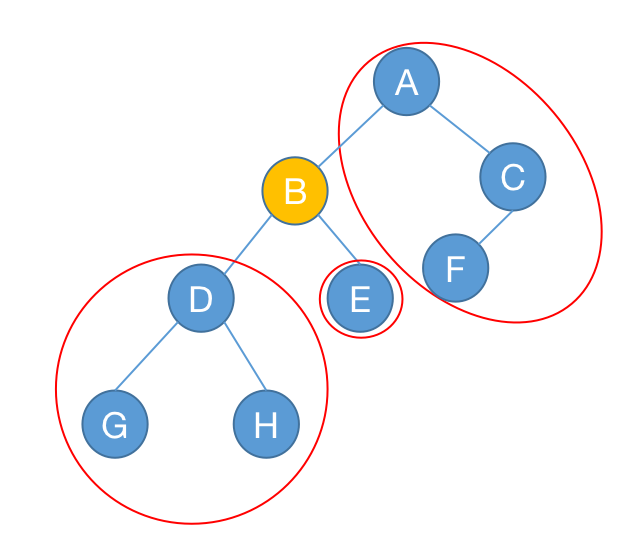
上式中，$v$ 为 $u$ 的每个儿子，我们枚举 $u$ 的每个儿子，并且统计以 $v$ 为根的子树的结点个数。最后再统计 $u$ 父亲部分构成的“子树”的结点个数。

求解出 $f$ 数组后，我们只需要找到 $f$ 值最小的结点即可。 $f$ 值最小的结点就是树的重心。

代码

int siz[maxn],f[maxn],n; // n 表示结点的数量
void dfs(int u, int fa) { // 表示搜索结点 u ，这个点的父亲为 fa
    siz[u] = 1; // 这个点本身就是一个结点，所以初始化为 1
    f[u] = 0;
    for (int i = head[u]; i; i = G[i].next) {
        int v = G[i].to;
        if (v == fa) { // 防止重复搜索
            continue;
        }
        dfs(v, u); // 先要计算出子树的 siz
        siz[u] += siz[v]; // 加上子树的结点数量
        f[u] = max(f[u], siz[v]); // 统计 f[u]
    }
    f[u] = max(f[u], n - siz[u]); // 统计父亲部分
}

树的直径

##### 网络延时 某计算机网络中存在 $n$ 个路由，每个路由代表一个子网。路由之间有 $n - 1$ 条互通关系，使得这 $n$ 个网络之间任意两个网络都可以直接联通，或者通过其他网络间接连通。
为了测试组建的网路的性能，假设相邻的路由之间的数据传输需要一单位时间，现在需要知道任意两个路由之间传输数据最多需要多长时间。

为了解决这道题目，我们引入 树的直径 的概念：

树的直径为树上最长简单路径（简单路径指不经过重复点、重复边的路径）

我们可以发现，树的直径一定是传输数据耗时最长的一条路径，所以我们只需要求出之这个网络的直径长度即可。

在树上任意选择一个结点 $i$，搜索树上距离结点 $i$ 最远的结点 $u$，然后再搜索距离结点 $u$ 最远的结点 $v$。此时 $u$ 到 $v$ 的路径即为树的直径。

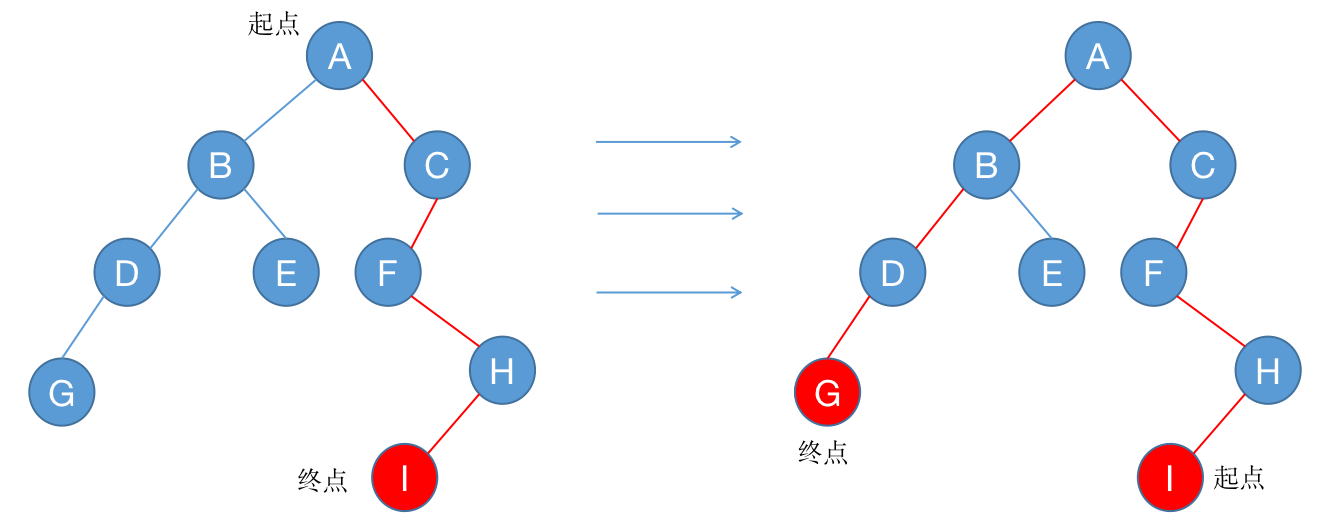
所以我们可以直接计算 $u$ 到 $v$ 的路径长度作为题目的答案，这个长度就是最远的两个路由之间传输数据最长需要的时间。

接下来我们看一下树的直径的算法证明，当然你只需要掌握计算方法，证明的内容学有余力的同学可以参考。

在这里我们只需要证明 $u$ 是直径的一端，因为我们可以用同样的方式证明 $v$ 是直径的一端（只需要把上一页中的点 $i$ 指定为 $u$）。我们使用反证法，假设通过上一页的算法求得的 $u$ 到 $v$ 的路径不是树的直径。

如果 $u$ 不是直径的一个端点，那么对于树上的直径 $(x,y)$：

1. $u$ 在 $x,y$ 的路径上：那么 $u$ 一定不是树上所有节点中距离 $i$ 最远的点。（因为 $x,y$ 至少有一个离 $i$ 的距离比 $u$ 更远）。
2. $u$ 不在 $x,y$ 的路径上且 $u,v$ 和 $x,y$ 有交点：
   • 令这个交点为 $p$。
   • 
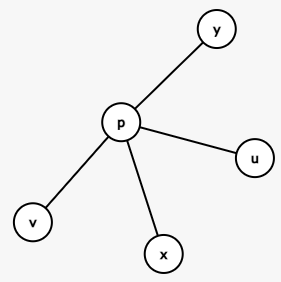
   • 那么肯定有 $dis(x,y)>dis(x,u),dis(x,v)$，同时减去 $dis(x,p)$，得到 $dis(p,y)>dis(p,u),dis(p,v)$。最后可以推出 $dis(p,u)+dis(p,y) > dis(p,u)+dis(p,v)$，即 $dis(u,y)>dis(u,v)$，和 $v$ 是树上距离 $u$ 最远的点矛盾。
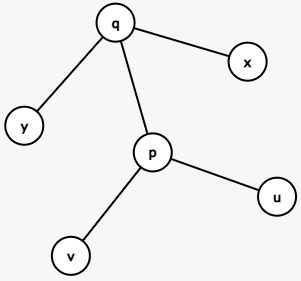
3. $u$ 不在 $x,y$ 的路径上且 $u,v$ 和 $x,y$ 没有交点：
   • $u,v$ 和 $x,y$ 没有交点：虽然我们分开讨论了，但是实际上这种情况和上一种情况在证明上是类似的。你需要在 $u,v$ 和 $x,y$ 的路径上分别找到点 $p,q$，使得路径 $(u,x),(u,y),(v,x),(v,y)$ 都会经过这两个点。然后你就可以按照刚才的方式去试着思考这种情况了。
   • 

不带权图算法

拓扑排序

排队问题

老师让同学们排成一队，准备带大家出去玩，一共有 $n$ 名同学。排队的时候同学们向老师提了 $m$ 条要求，每一条要求是说同学 $x$ 一定要排在同学 $y$ 之前，老师现在想找到一种排队方式可以满足所有的要求，你能帮帮他吗？

我们考虑如何找到一个合法的排队方式：

我们维护一个队列，队列内维护的是已经排好队的同学，初始时这个队列是空的，每次让一个同学进入到队列的尾部（后面我们称这个动作为“进入队列”），当 $n$ 名同学都进入队列后，排队就完成了。

可以发现，当一个同学进入队列时，所有要求排在他之前的同学需要已经进入队列。

我们将题目中的要求转化为图的形式来表示：

• 每个编号为 $i$ 的同学用编号为 $i$ 的点来表示
• 一个同学 $x$ 一定要排在同学 $y$ 之前的要求用一条由 $x$ 指向 $y$ 的有向边来表示。

如图：

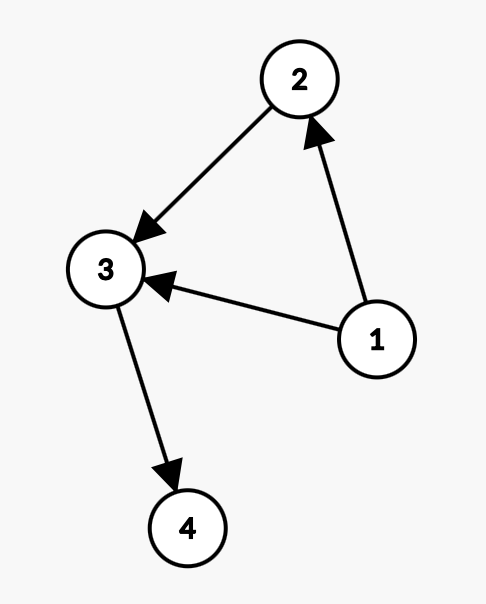
表示有 $4$ 个同学，有 $4$ 条要求，分别是：

• $1$ 应该先于 $2$ 进入队列
• $1$ 应该先于 $3$ 进入队列
• $2$ 应该先于 $3$ 进入队列
• $3$ 应该先于 $4$ 进入队列

DAG

可以发现，我们这样画出的图中不会存在环，否则无法找到满足所有要求的一种队列。这样的图我们称为有向无环图(DAG, directed acyclic graph)

之后我们会介绍用于求解这个排队问题的算法: 拓扑排序。

求解排队问题

假设我们现在要对这个图表示的排队问题进行求解：

我们考虑能否让 $2$ 第一个进入队列。观察上图可以发现，有一条 $1→2$ 的有向边，表示 $2$ 进入队列之前需要先让 $1$ 进入队列。所以 $2$ 不能第一个进入队列。

通过上面的判断方式，我们发现可以根据一个点的入边来判断这个点进入队列前需要哪些点已经进入队列。

拓扑排序就是依照这个原理进行的，但是拓扑排序将这个判断过程简化为了对入度的判断。通过只判断入度，可以在保证正确性的情况下简化算法流程。

拓扑排序

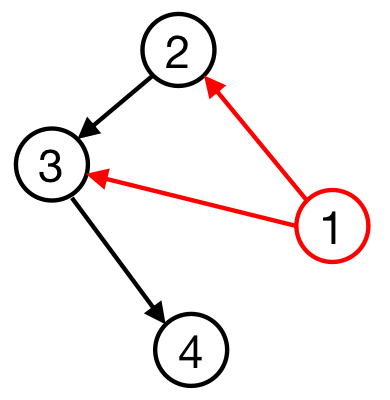
对于一个有向图，拓扑排序的运算流程如下：

1. 找到一个入度为 $0$ 的顶点，将这个顶点加入到拓扑序的尾部。
2. 删除步骤 $1$ 中找到的点以及以该点作为起点的所有有向边。
3. 回到步骤 $1$ ，直到步骤 $1$ 找不到满足要求的顶点为止。

算法中提到了拓扑序这一名词，实际上拓扑序的定义与题目要求的排队序列定义相同，就是指满足该图要求的一种序列。

算法的终止有两种情况：

• 该图变成了空图，没有顶点存在。此时我们会得到一个正确的拓扑序
• 该图不是空图，但是找不到入度为 $0$ 的结点。此时我们可以确定这个图中存在至少一个有向环，不存在拓扑序。

所以，拓扑排序不仅可以用于求解拓扑序，也可以用于判断一个有向图中是否存在有向环。

接下来我们模拟运行一下拓扑排序在下图中的运行情况：

初始化：

拓扑序 : []

顶点编号	1	2	3	4
入度	0	1	2	1

第 $1$ 次迭代:

拓扑序 : [1]

顶点编号	1	2	3	4
入度	被删除	1	2	1

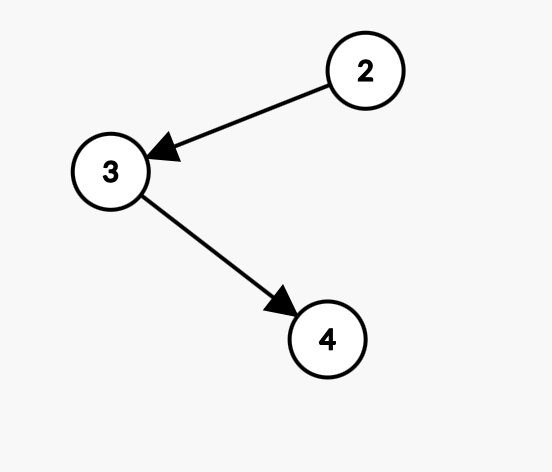
第 $2$ 次迭代：

拓扑序 : [1,2]

顶点编号	1	2	3	4
入度	被删除	被删除	0	1

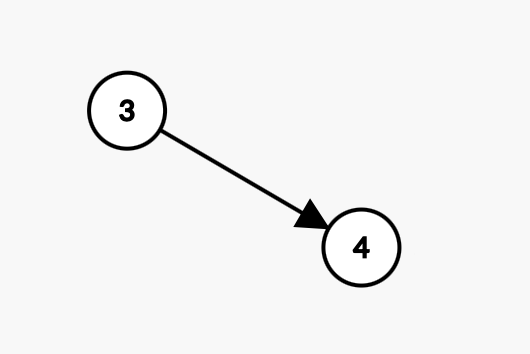
第 $3$ 次迭代：

拓扑序 ： [1,2,3]

顶点编号	1	2	3	4
入度	被删除	被删除	被删除	0

第 $4$ 次迭代：

拓扑序 : [1,2,3,4]

顶点编号	1	2	3	4
入度	被删除	被删除	被删除	被删除

第 $5$ 次迭代：

没有找到符合要求的顶点，算法退出。

最终的拓扑序即为： [1,2,3,4]

参考代码

bool toposort(int n){
    priority_queue<int, vector<int>, greater<int> > q;
    for (int i = 1; i <= n; i++) {
        if(deg[i] == 0) {
            q.push(i);
        }
    }
    int ncnt = 0;
    while (!q.empty()) {
        int u = q.top();
        q.pop();
        seq[++ncnt] = u;
        for (int i = 0; i < G[u].size(); i++){
            int v = G[u][i];
            deg[v] -= 1;
            if(deg[v] == 0) {
                q.push(v);
            }
        }
    }
    return ncnt == n;
}

拓扑排序的一些应用

我们这里使用了一道题目来讲解拓扑排序算法，实际上这个算法的作用就是用于求解出一组特定的序列，这个序列满足所有的顺序要求。

例如我们之后会学习到的 在 DAG 上 DP，就需要使用拓扑序来进行更新转移。

拓扑排序一般都与其他算法一同使用，用于求解一个较为复杂的问题。

除了求解序列之外，拓扑序列还可以用于判断一个图是不是 DAG，具体的判别法我们在讲解拓扑排序的终止状态时提到了。

欧拉路与欧拉回路

七桥问题

全名柯尼斯堡七桥问题(Seven Bridges of Königsberg)是图论中的著名问题。这个问题是基于一个现实生活中的事例：当时东普鲁士柯尼斯堡市区跨普列戈利亚河两岸，河中心有两个小岛。小岛与河的两岸有七条桥连接。在所有桥都只能走一遍的前提下，如何才能把这个地方所有的桥都走遍？

我们用图论来思考这个问题：在一个有 $n$ 个顶点的无向连通图中，能否找到一条路径，使得每条边都被刚好经过一次。

• 满足这个条件的路径我们称之为 欧拉路径。
• 如果某个欧拉路径的起点与终点是相同的点，那么这个路径为 欧拉回路。

需要注意的是，欧拉路径只要求不经过重复的边，经过重复的点是允许的。

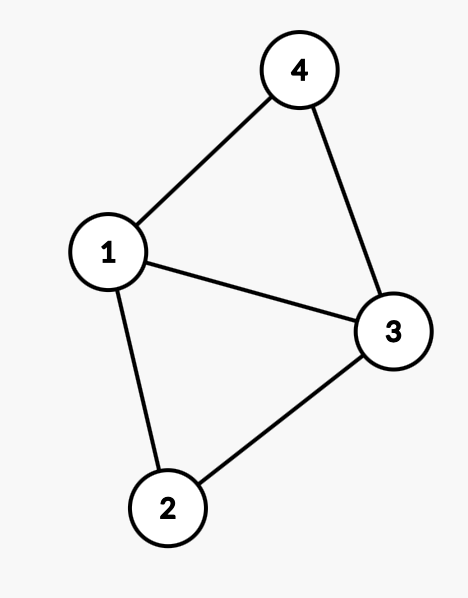
例如下图的欧拉路径可以为：$1\to 2 \to 3 \to 1 \to 4 \to 3$

欧拉图的判定

欧拉图

让我们来了解一下 欧拉图 的定义：

• 具有欧拉回路的图称为 欧拉图。
• 具有欧拉路径但不具有欧拉回路的图称为 半欧拉图。

无向欧拉图的判定

让我们回到最初的七桥问题，实际上就是判断该图是否是半欧拉图。也就是判断这张图是否存在欧拉路径或欧拉回路。

关于这个问题，欧拉给出了判别法：

• 对于无向图 $G$，$G$ 是欧拉图当且仅当 $G$ 是连通的且没有度数为奇数的顶点
• 对于无向图 $G$，$G$ 是半欧拉图当且仅当 $G$ 是连通的且有两个度数为奇数的顶点

我们来通俗地理解一下，每一个度数都代表要从这个点经过一次，或从这个点离开，或进入这个点。

对于欧拉回路来说，进入一个点的次数和离开该点的次数需要相等，这样才能满足回路的性质，所以要求每个点的度数都为偶数。

对于欧拉路径来说，需要一个起点和终点，离开起点的次数需要比进入起点多 $1$ 。相应的，进入终点的次数也应该比离开终点的次数多 $1$。所以起点与终点的度数应该为奇数。

现在让我们判断一下最初的七桥问题，我们可以用该图来描述它：

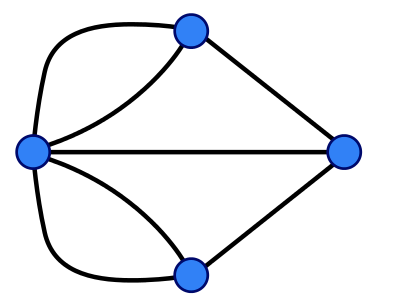
可以发现，图中的四个点度数分别为：$5,3,3,3$，有 $4$ 个度数为奇数的顶点，所以其既不是欧拉图也不是半欧拉图，七桥问题是无解的。

有向欧拉路的判定

有向图中欧拉路径的定义与无向图的定义相同，与之不同的是：有向边规定了只能从特定方向来通过这条边。

在有向图的情况下，我们需要使用点的出度和入度来进行判断：

• 对于有向图 $G$ , $G$ 是欧拉图当且仅当 $G$ 是连通的且所有的点的入度和出度相同
• 对于有向图 $G$ , $G$ 是半欧拉图当且仅当 $G$ 满足：
  1. 图连通
  2. 恰好有一个点入度比出度多 $1$
  3. 恰好有一个点出度比入度多 $1$
  4. 除了 $2,3$ 点中的点，其他的点入度与出度相同

求解欧拉路径

求解无向图欧拉路径

我们前面学习了如何判断是否存在欧拉路径，现在我们来学习如何求出欧拉路径。

求解欧拉路径时，我们可以采用 DFS 的方式来求。

从一个 合适的顶点 出发（合适的顶点的定义会在后面给出），进行 DFS。当到达一个顶点 $u$ 时：

1. 如果该顶点没有与任何边相连，则将 $u$ 加入到欧拉路径中并且回溯。
2. 找到一条与 $u$ 相连的边，假设该边连接 $to$ 。删除该边，并且递归搜索顶点 $to$ 。
3. 重复进行第二步，直到找不到与 $u$ 相连的边，将 $u$ 加入到欧拉路径中并且回溯。

const int maxn = 105;
const int maxm = 10005;
int degree[maxn];  // 表示顶点剩余的度
int n;  // 顶点个数
struct edge {
    int next, to, vis;
} Edge[maxm * 2];
int h[maxn], tot = -1;
void dfs(int u) {
    if (degree[u]) {
        for (int i = h[u]; i != -1; i = Edge[i].next) {
            if (!Edge[i].vis) {
                int to = edge[i].to;
                Edge[i].vis = true;
                int fedge;
                if (i % 2 == 0) {
                  fedge = i + 1;
                } else {
                  fedge = i - 1;
                }
                Edge[fedge].vis = true; // 标记反向边
                degree[u]--;
                degree[to]--;
                dfs(to);
            }
        }
    }
    cout << u << endl;
}

求解有向图欧拉路径

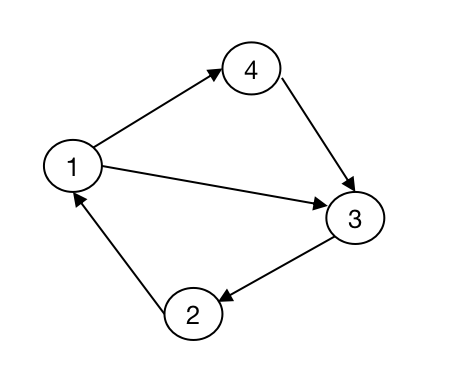
与求解无向图的欧拉路径的算法类似，但是要注意：

1. 在进行有向图搜索时，我们需要通过判断顶点的出度来判断该点是否连出了边。
2. 不能直接输出欧拉路径，我们需要将这个路径逆序输出。可以在每次得到欧拉路径的顶点时将该点压入栈中，然后再依此取栈顶元素并且输出。

const int maxn = 105;
const int maxm = 10005;
int out[maxn];  // 表示顶点剩余的度
int n;  // 顶点个数
struct edge {
    int next, to, vis;
} Edge[maxm * 2];
int h[maxn], tot = -1;
stack<int> s;
void dfs(int u) {
    if (out[u]) {
        for (int i = h[u]; i != -1; i = Edge[i].next) {
            if (!Edge[i].vis) {
                int to = edge[i].to;
                Edge[i].vis = true;
                out[u]--;
                dfs(to);
            }
        }
    }
    s.push(u);
}

我们在算法中提到了 一个合适的顶点 ，那么什么是合适的顶点呢？

如果图中存在欧拉回路，那么我们可以从任意结点开始搜索，都可以求出正确的欧拉路径。

如果图中不存在欧拉回路，只有欧拉路径，我们就需要找到度数为奇数的顶点（有向图中需要找到出度比入度大 $1$ 的顶点），作为起点来进行搜索。

图论建模

SPFA 判断负权环

我们学习过 Floyd、Dijkstra、SPFA 求解最短路。

但是 Dijkstra 不能处理有负权的图，而 SPFA 可以处理任意不含负环（负环是指总边权和为负数的环）的图 的最短路，并能 判断图中是否存在负环。

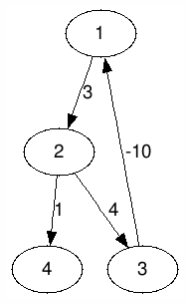
上图就存在 $1\to 2\to 3\to 1$ 这样一个负环，一直沿着负环走下去，最短路径会越来越小，趋向于负无穷大。所以存在负环的时候，SPFA 算法无法停止下来。

但是 SPFA 可以用来判断负环，在进行 SPFA 时，用一个数组 $cnt_i$ 来标记每个顶点 入队 次数。如果一个顶点入队次数 $cnt_i$ 大于等于顶点总数 $n$，则表示该图中包含负环。

这个问题我们可以这样考虑：一个点 $i$ 如果多次入队，那么某一次入队相对于上一次入队必定满足：该次入队时从起点到 $i$ 的路径上边的条数必定比上一次至少多了 $1$。

由此可得，如果进队次数大于 $n$ 次，那么就说明起点到点 $i$ 的最短路径上的边的条数是大于等于 $n$ 的。而 $n$ 个点不成环的时候路径上的边数最多是 $n-1$，所以 $i$ 进队次数达到 $n$ 次时，从起点到 $i$ 的最短路径上必然有环，而根据最短路的定义，这个环上边的权值和必然是负数。

一般情况下，SPFA 判负环都只用在有向图上，因为在无向图上，一条负边权的边就是一个负环了。

最短路建模方法总结

前面我们学习过一些求解最短路的算法。

图是由点和边组成，那么我们在最短路建模的过程中，需要从题目中提取出重要信息：

1. 有/无向图；
2. 是否存在负权边；
3. 是否需要反向建图；

常见的最短路问题模型包括：

1. 单源最短路问题

   • 存在负权边：可以使用 SPFA 算法
   • 不存在负权边：可以使用 Dijkstra、SPFA 算法

2. 多源到单源最短路问题

   通过反向建图，求出从终点到其他点的最短路。

3. 任意两点之间的最短路问题

   可以通过 Floyd 算法求解。

4. （非严格）次短路

   • 不可以经过重复点：找到最短路径，依次枚举删除路径中的每一条边，再求解最短路，维护最小值。

   • 可以经过重复点： 在 Dijkstra 算法的基础上，维护从起点 $s$ 到达其他每个点 $v$ 的最短路 $dis_1[v]$ 和次短路 $dis_2[v]$。对于边 $u\stackrel{w}{\longrightarrow} v$： \(dis_2[v]=\begin{cases} dis_2[u] + w& \\dis_1[u] + w \\dis_1[v]\end{cases}\)

5. 最短路变形

   • 最长边最短：改造 Floyd 算法的松弛公式：Map[i][j] = min(Map[i][j], max(Map[i][k], Map[k][j]));
   • 最短边最长：改造 Floyd 算法的松弛公式：Map[i][j] = max(Map[i][j], min(Map[i][k], Map[k][j]));

算法选择

下表为在 $N$ 个点，$M$ 条边的图中不同最短路算法的特性。其中 $k$ 表示平均入队次数为，对于较为随机的稀疏图，根据经验 $k$ 一般不超过 $4$。 | 算法 | Floyd | Dijkstra | 堆优化 Dijkstra | SPFA | | — | — | — | — | — | | 时间复杂度 | $\mathcal{O}(N ^ 3)$ | $\mathcal{O}(N^2)$ | $\mathcal{O}((N + M)\log N)$ | $\mathcal{O}(kM)$ | | 使用情况 | 多源最短路 | 单源最短路 | 单源最短路 | 单源最短路 | | 负权边 | 可以处理负权边 | 不能处理负权边 | 不能处理负权边 | 可以处理负权边，可以判断负权环 |

一般情况下，需要根据数据特性（数据范围、是否存在负权边）选择合适的最短路算法。

最小生成树建模方法总结

前面我们学习了两种求解最小生成树的方法。

下表为在 $n$ 个点，$m$ 条边的图中不同最小生成树解法的特性。

算法	Kruskal	Prim
时间复杂度	$\mathcal{O}(m\log m)$	$\mathcal{O}(n^2)$（朴素） $\mathcal{O}((n+m)\log m)$（堆优化）
适用范围	无向图	无向图、有向图

最小生成树的本质是一棵树，$n$ 个结点共有 $n-1$ 条边。一般情况下是要求在一个图中，求出权值最小的连通图。

最小生成树建模

问题一： $n$ 个点，$m$ 条带权无向边，怎么求出生成树中最大边与最小边之差最小的值。

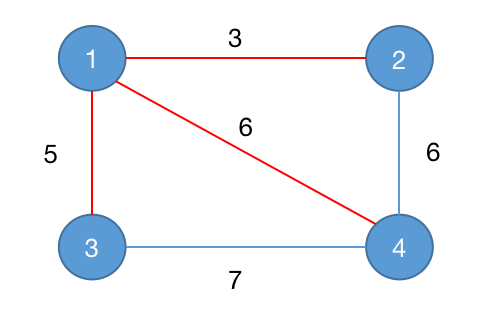
我们考虑 Kruskal 算法：首先按照边权从小到大排序。然后依次枚举每一条边作为生成树的最小边，继续向后求解生成树，当生成树构建完成时，最后使用的边就是最大边，此时就能够求出一系列的差值，维护最小差值即可。

所以本题的本质上还是使用 Kruskal 算法构造生成树。

问题二：《安慰奶牛》

Farmer John 变得非常懒，他不想再继续维护供奶牛之间供通行的道路。道路被用来连接 $N$ 个牧场，牧场被连续地编号为 $1$ 到 $N$。每一个牧场都是一个奶牛的家。FJ 计划除去 $P$ 条道路中尽可能多的道路，但是还要保持牧场之间的连通性。

你首先要决定那些道路是需要保留的 $N-1$ 条道路。第 $j$ 条双向道路连接了牧场 $S_j$ 和 $E_j$($1 \leq S_j \leq N; 1 \leq E_j \leq N; S_j \neq E_j$)，而且走完它需要 $L_j$ 的时间。没有两个牧场是被一条以上的道路所连接。奶牛们非常伤心，因为她们的交通系统被削减了。你需要到每一个奶牛的住处去安慰她们。每次你到达第 $i$ 个牧场的时候(即使你已经到过)，你必须花去 $C_i$ 的时间和奶牛交谈。你每个晚上都会在同一个牧场(这是供你选择的)过夜，直到奶牛们都从悲伤中缓过神来。在早上起来和晚上回去睡觉的时候，你都需要和在你睡觉的牧场的奶牛交谈一次。这样你才能完成你的 交谈任务。假设 Farmer John 采纳了你的建议，请计算出使所有奶牛都被安慰的最少时间。

输入格式

第 $1$ 行包含两个整数 $N(5\leq N \leq 10^4)$ 和 $P(N-1\leq P \leq 10^5)$。

接下来 $N$ 行，每行包含一个整数 $C_i(1\leq C_i \leq 1000)$。

接下来 $P$ 行，每行包含三个整数 $S_j, E_j$ 和 $L_j$。

输出格式

输出一个整数，所需要的总时间(包含和在你所在的牧场的奶牛的两次谈话时间)。

样例输入

5 7
10
10
20
6
30
1 2 5
2 3 5
2 4 12
3 4 17
2 5 15
3 5 6
4 5 12

样例输出

176

题意：有 $N$ 个点，$P$ 条无向边。每到达一个点需要在这个点上停留 $C_i$ 时间，每条边 $u\leftrightarrow v$ 需要消耗 $L_i$ 的时间。现在想要求从任意一点，走遍所有点，并且再回到出发点的最少消耗时间？

因为最后剩下的边会构成一棵树，想要最少的消耗时间，所以我们能够想到最小生成树。

不过因为要返回到起点，所以最小生成树的每条边都要走两遍，并且还需要加上边的两个端点的权值 $C_u,C_v$。故，我们调整每条边的边权值：$newL_{u\leftrightarrow v} = 2\times L_{u\leftrightarrow v} + C_u + C_v$。 然后在新图中求解最小生成树的权值和即可。

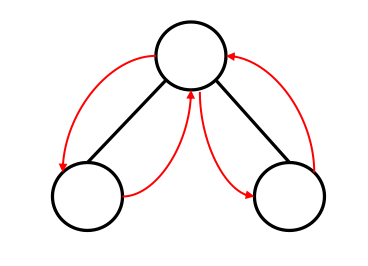
需要注意的是：因为是从起点出发，最后再回到起点，那么可以假设起点为树的根结点。如果按照上述方法重新处理边权的话，少算了一次根结点的权值。所以答案应该为：最小生成树的边权和 + 根结点的权值。

因为最小生成树的边权和是固定的，故根结点应该为权值最小的点。

次小生成树

（非严格）次小生成树：设 $G = (V, E)$ 是连通的无向图，$T$ 是图 $G$ 的一个最小生成树。如果有另外一棵树 $T_1,T_1 \neq T$，满足不存在树 $T’,T’ \neq T,w(T’) < w(T_1)$，则称 $T_1$ 是图 $G$ 的次小生成树。

算法一：

先求最小生成树，再枚举删去最小生成树中的边，再求解最小生成树；时间复杂度为：$\mathcal{O}(nm\log m)$。

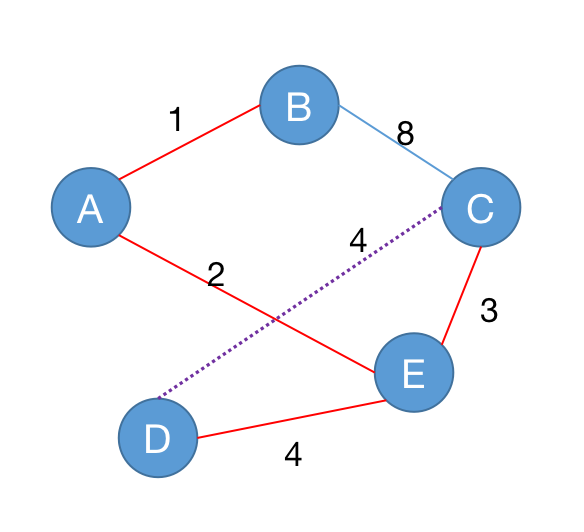
算法二：

$T$ 为图 $G$ 的一棵生成树，对于非树边 $a$ 和树边 $b$，插入边 $a$ 并删除边 $b$ 的操作记为 $(+a,-b)$。

如果 $T+a-b$ 仍然是一棵生成树，称 $(+a,-b)$ 是 $T$ 的一个可行交换。

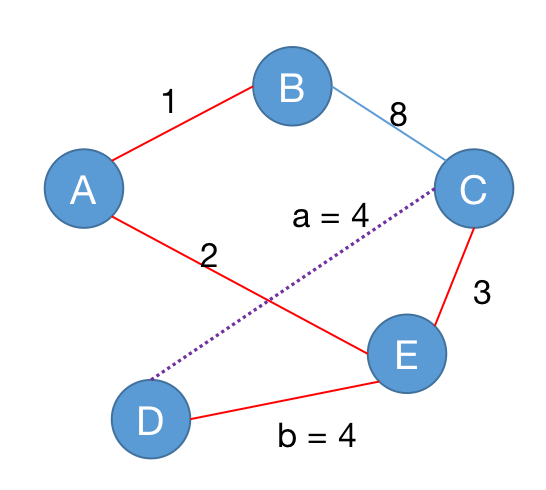
设 $T$ 为图 $G$ 的一棵生成树，由 $T$ 进行一次可行交换得到的新的生成树集合称为 $T$ 的邻集。

定理：次小生成树在最小生成树的邻集中。

关键问题：如何快速计算邻集中的最小树。

枚举加边 $(u,v)$，则形成唯一的环，它由 $u\to v$ 在树中的唯一路径，加上 $(u,v)$ 边构成，由于在邻集中最小的一棵生成树为次小生成树，只需考虑删除环中的最大边。

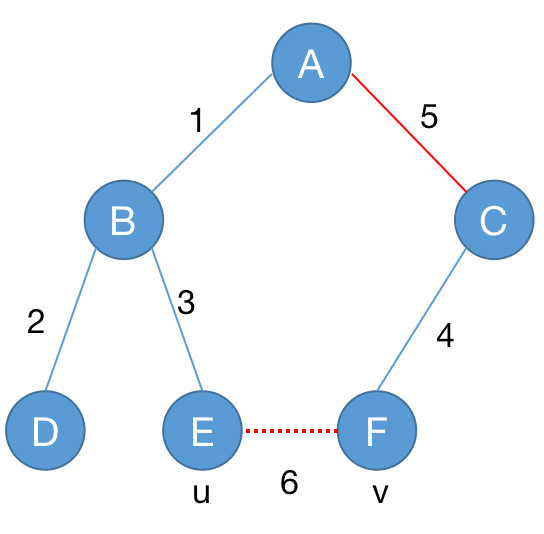
算法二：

具体操作

1. 设 $Max[i][j]$ 表示在最小生成树中任意两个点 $i,j$ 的唯一路径中权值最大的那条边的权值。 $Max[][]$ 可以由 $\mathcal{O}(n^2)$ 求出。

2. 枚举所有不在最小生成树 $T$ 中的边 $(i,j)$，加入边 $(i,j)$ 替换权为 $Max[i][j]$ 的边，即当前最小生成树的权值 $Ans= Ans+ map[i][j]- Max[i][j]$。

3. 不断更新生成树的最小值，即可求出次小生成树。

总的时间复杂度为 $\mathcal{O}(n^2 +m)$。

基础树上 DP

树上动态规划

树形动态规划，就是在树这一特殊的结构上维护、更新状态的最优解。

通常，我们从根结点出发，向子结点进行深度优先搜索，并由其子结点的最优解合并得到该结点的最优解。

比如，我们现在需要计算每棵子树 $u$ 中所有结点的最大权值 $Max[u]$，假设结点 $u$ 的权值为 $val[u]$，首先遍历其所有子结点 $v = children[u]$，再由子结点的 $Max[v]$ 更新得到最大值，即：$Max[u]=\max(Max[v],val[u]) ,v\in children(u)$。

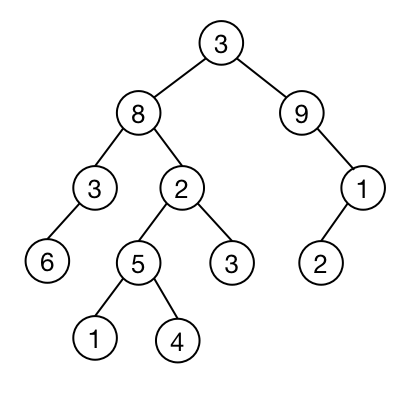
有些问题，我们还需再次从根结点出发，向子结点进行深度优先搜索。对于树上的每个结点（除根结点以外），由父结点的信息（父结点合并后的信息，除去该孩子的信息，就是其余孩子的信息）更新该结点的信息。

例题：奇怪的花卉

小明对数学饱有兴趣，并且是个勤奋好学的学生，总是在课后留在教室向老师请教一些问题。一天他早晨骑车去上课，路上见到一个老伯正在修剪花花草草，顿时想到了一个有关修剪花卉的问题。于是当日课后，小明就向老师提出了这个问题：

一株奇怪的花卉，上面共连有 $N$ 朵花，共有 $N-1$ 条枝干将花儿连在一起，并且未修剪时每朵花都不是孤立的。每朵花都有一个“美丽指数”，该数越大说明这朵花越漂亮，也有“美丽指数”为负数的，说明这朵花看着都让人恶心。所谓“修剪”，意为：去掉其中的一条枝条，这样一株花就成了两株，扔掉其中一株。经过一系列“修剪“之后，还剩下最后一株花（也可能是一朵）。老师的任务就是：通过一系列“修剪”（也可以什么“修剪”都不进行），使剩下的那株（那朵）花卉上所有花朵的“美丽指数”之和最大。

老师想了一会儿，给出了正解。小明见问题被轻易攻破，相当不爽，于是又拿来问你。

输入格式

第一行一个整数 $N\ (1 \le N \le 16000)$，表示原始的那株花卉上共 $N$ 朵花。

第二行有 $N$ 个整数，第 $i$ 个整数 $a_i\ (-10^4\le a_i \le 10^4)$表示第 $i$ 朵花的美丽指数。

接下来 $N-1$ 行每行两个整数 $a,b$，表示存在一条连接第 $a$ 朵花和第 $b$ 朵花的枝条。

输出格式

一个数，表示一系列“修剪”之后所能得到的“美丽指数”之和的最大值。

样例输入

7
-1 -1 -1 1 1 1 0
1 4
2 5
3 6
4 7
5 7
6 7

样例输出

3

解析

树上问题往往从根结点开始，由子树逐渐往上更新到整棵树。

这里我们不妨先设 $1$ 为根。设 $dp[u]$ 表示以 $u$ 为根的子树在保留 $u$ 节点的情况下完成“修剪“后”美丽指数”之和最大是多少。

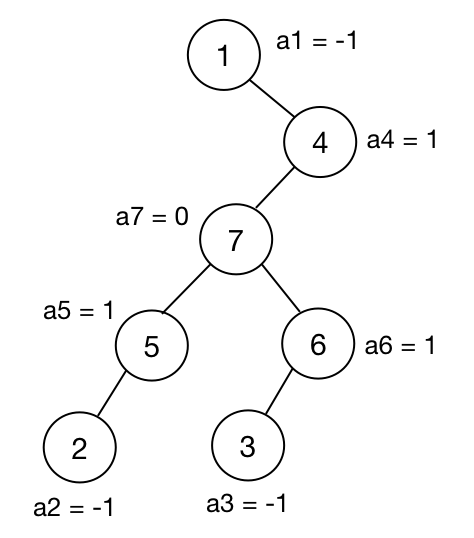
转移时我们发现如果对于 $u$ 的子节点 $v$，有 $dp[v] > 0$，那么 $(u, v)$ 这条边就不该剪，所以状态转移方程为：

$dp[u] = a[u] + \sum_{dp[v] > 0} dp[v]$

我们找到 $dp$ 数组的最大值即可。

参考代码

#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 16010;
vector <int> G[maxn];
int a[maxn], dp[maxn];
void addedge(int u, int v) {
    G[u].push_back(v);
}
int dfs(int u, int fa) {
    dp[u] = a[u];
    for (int i = 0; i < G[u].size(); i++) {
        int v = G[u][i];
        if (v != fa && dfs(v, u) > 0) {
            dp[u] += dp[v];
        }
    }
    return dp[u];
}
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    for (int i = 0; i < n - 1; i++) {
        int u, v;
        cin >> u >> v;
        addedge(u, v);
        addedge(v, u);
    }
    dfs(1, 0);
    int ans = -inf;
    for (int i = 1; i <= n; i++) {
        ans = max(ans, dp[i]);
    }
    cout << ans << endl;
    return 0;
}

树上的最小点覆盖

在一棵树上选出最少的点，使得每一条边都至少被一个点覆盖。

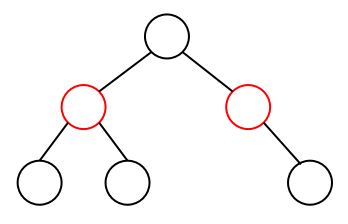
解析

树上的最小点覆盖可以用动态规划来求解。用 $dp[u][0]$ 表示不选择 $u$ 的情况下，$u$ 及其子树完全被覆盖需要的最少的点，$dp[u][1]$ 表示选择 $u$ 的情况下，$u$ 及其子树完全被覆盖需要的最少的点。

那么对于 $u$ 的儿子 $v$ 有转移：

• 如果不选择点 $u$，那么所有子结点 $v$ 都要被选，用来覆盖边 $<u, v>$

\[dp[u][0] = \sum_{v} dp[v][1]\]

• 如果选择点 $u$，那么子结点可以选可以不选，只需要取最小值即可。

\[dp[u][1] = \sum_v \min(dp[v][0], dp[v][1]) + 1\]

若 $x$ 为叶子结点，则： $dp[x][0] = 0,dp[x][1] = 1$；

按点计算贡献

在树上求一个算式的值，其中涉及到求和的时候，有时我们可以按照每个点的点权在其中出现了多少次，即每个点对该算式的贡献分别计算后再求和。

接下来我们来看这样一个问题。

[NOIP 2014] 联合权值

无向连通图 $G$ 有 $n$ 个点，$n-1$ 条边。点从 $1$ 到 $n$ 依次编号，编号为 $i$ 的点的权值为 $W_i$，每条边的长度均为 $1$。图上两点 $(u, v)$ 的距离定义为 $u$ 点到 $v$ 点的最短距离。对于图 $G$ 上的点对 $(u, v)$，若它们的距离为 $2$，则它们之间会产生 $W_u \times W_v$ 的联合权值。

请问图 $G$ 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入格式

第一行包含 $1$ 个整数 $n$。

接下来 $n-1$ 行，每行包含 $2$ 个用空格隔开的正整数 $u$、$v$，表示编号为 $u$ 和编号为 $v$ 的点之间有边相连。

最后 $1$ 行，包含 $n$ 个正整数，每两个正整数之间用一个空格隔开，其中第 $i$ 个整数表示图 $G$ 上编号为 $i$ 的点的权值为 $W_i$。

输出格式

输出共 $1$ 行，包含 $2$ 个整数，之间用一个空格隔开，依次为图 $G$ 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对 $10007$ 取余。

数据范围

对于 $30$% 的数据，$1< n \le100$；

对于 $60$% 的数据，$1< n \le 2000$；

对于 $100$% 的数据，$1< n \le 200,000$，$0<Wi \le 10,000$。

样例说明

本例输入的图如上所示，距离为 $2$ 的有序点对有 $(1,3)$、$(2,4)$、$(3,1)$、$(3,5)$、$(4,2)$、$(5,3)$。其联合权值分别为 $2$、$1> 5$、$2$、$20$、$15$、$20$。其中最大的是 $20$，总和为 $74$。

输入样例

5
1 2
2 3
3 4
4 5
1 5 2 3 10

输出样例

20 74

解析

这个题是求一棵树上，所有距离为 $2$ 的点对的点权的乘积的和，以及所有距离为 $2$ 的点对的点权的乘积的最大值。如果用暴力写，枚举中间点，那实际求的两个点一定是与这个中间点相连的，暴力枚举这两个点，会发现在一种特殊的情况下，所有点都和一个点相邻，复杂度就会达到平方，就会超时。

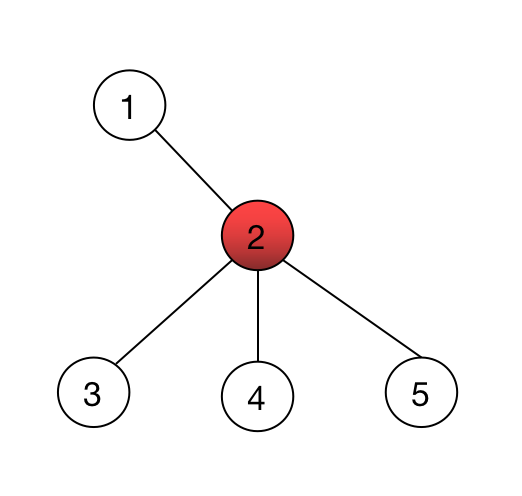
对于最大值，比较简单，在枚举中间点以后就可以直接取两个最大的相乘。

对于和，比较麻烦，可以这样优化，考虑如何快速计算以每个点为中间点的结果，会发现当枚举了其中一个点的时候，另一个点一定可以是中间点相连的除了已经枚举的那个点以外的所有点。所以可以在枚举中间点的基础上再枚举其中一个点，乘上其他与中间点相邻的点的权值和，这个权值和可以通过所有与中间点相邻的点的权值和减掉枚举的这个点的权值得到。

这样总复杂度降到了 $\mathcal{O}(n)$ 。

参考代码

#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int mod = 10007;
const int maxn = 200005;
vector < int > G[maxn];
void addedge(int u, int v) {
    G[u].push_back(v);
}
int S[maxn];
int W[maxn];
int n, maxx, sum;
int main() {
    cin >> n;
    for (int i = 0; i < n - 1; i++) {
        int u, v;
        cin >> u >> v;
        addedge(u, v);
        addedge(v, u);
    }
    for (int i = 1; i <= n; i++) {
        cin >> W[i];
    }
    for (int i = 1; i <= n; i++) {
        int max1 = 0, max2 = 0;
        max1 = 0;
        max2 = 0;
        for (int j = 0; j < G[i].size(); j++) {
            S[i] = (S[i] + W[G[i][j]]) % mod;
            if (W[G[i][j]] >= max1) {
                max2 = max1;
                max1 = W[G[i][j]];
            } else if (W[G[i][j]] > max2) {
                max2 = W[G[i][j]];
            }
        }
        maxx = max(maxx, max1 * max2);
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j < G[i].size(); j++) {
            sum = (sum + (S[i] - W[G[i][j]] + mod) * W[G[i][j]]) % mod;
        }
    }
    cout << maxx << " " << sum << endl;
    return 0;
}

按边计算贡献

在树上除了点以外，边也很重要。对于一个算式，有时我们可以按照每个边的边权在算式中出现了多少次，即每个边对该算式的贡献分别计算后再求和。

接下来我们来看这样一个问题。

战后重建

世界大战后，世界各国都变成了废墟，S国同样也未能避免战火，所有的道路和村庄都被炸毁。S国国王很清楚，要想加快国家建设，恢复以前的繁荣，第一件需要做的事情就是修路（要想富先修路）。

S国有 $n$ 个村庄，编号从 $1$ 到 $n$ ，S国国王计划出了 $m$ 条道路的建设，每条道路长 $w_i$ ，$w_i$ 各不相同，这些道路直接或间接的把所有的村庄连接起来。但国家需要用钱的地方还有很多，所以S国国王想使用最少的花费把所有的村庄连接起来（距离等于花费）。在这基础上S国国王还提出了一个问题，选择任意两个不同的点作为起点和终点，都会有一个距离，这些距离的总和是多少？

注意：起点为 $a$，终点为 $b$ 和起点为 $b$，终点为 $a$ 两种情况只记一次。

输入格式

第一行输入两个整数 $n,\ m$，分别表示村庄数目和计划建设的道路数目。

接下来 $m$ 行，每行有三个整数 $x,\ y,\ w_i$ ，表示计划在村庄 $x$ 和村庄 $y$ 之间建设一条长度为 $w_i$ 的道路。

数据范围： $1 \le n \le 10^5$ , $1 \le x,\ y \le n$ , $1 \le m ,\ w_i \le 10^6$ 。

输出格式

输出两个整数，中间以空格隔开，第一个数表示最小的花费，第二个数表示距离的总和。

样例输入

4 6
1 2 1
2 3 2
3 4 3
4 1 4
1 3 5
2 4 6

样例输出

6 20

解析

对于第一问，就是最小生成树，可以使用 Kruskal 算法建树。

对于第二问，如果我们通过最短路计算会超时，换个思路想，每条道路乘以它的使用次数就是总和 $sum$ ，使用次数是这条道路左边的村庄数乘以右边的村庄数。

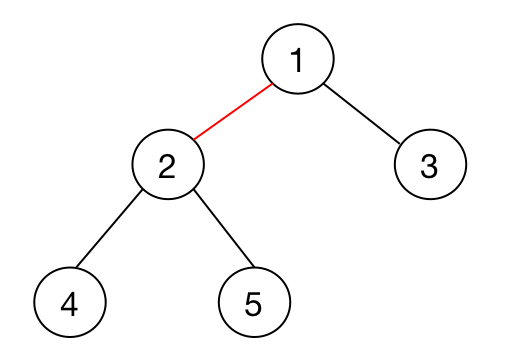
设在 DFS 的过程中 $u$ 是 $v$ 的父亲，那么 $v$ 这一侧的村庄数就是 $v$ 的子树大小，$u$ 这一侧的村庄数就是 $n$ 减去 $v$ 的子树大小。

那么 $(u, v)$ 这条边的使用次数就是 $size[v] \times (n - size[v])$ 。

参考代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int maxn = 100005;
int n, m, u, v, w;
struct edge {
    int v;
    int w;
};
int fa[maxn], sz[maxn];
vector<edge> G[maxn];
long long ans;
void addedge(int u, int v, int w) {
    G[u].push_back(edge{v, w});
}
struct node {
    int u;
    int v;
    int w;
};
node g[1000005];
bool cmp(node x, node y) {
    return x.w < y.w;
}
void init() {
    ans = 0;
    for (int i = 1; i <= n; i++) {
        fa[i] = i;
    }
}
int get(int x) {
    if (fa[x] != x) {
        fa[x] = get(fa[x]);
    }
    return fa[x];
}
bool merge(int x, int y) {
    int fx = get(x);
    int fy = get(y);
    if (fx == fy) {
        return false;
    }
    fa[fx] = fy;
    return true;
}
long long kruskal() {
    sort(g, g + m, cmp);
    long long res = 0;
    for (int i = 0; i < m; i++) {
        if (merge(g[i].u, g[i].v)) {
            addedge(g[i].u, g[i].v, g[i].w);
            addedge(g[i].v, g[i].u, g[i].w);
            res += g[i].w;
        }
    }
    return res;
}
int dfs(int u, int fa) {
    for (int i = 0; i < G[u].size(); i++) {
        if (G[u][i].v != fa) {
            sz[u] += dfs(G[u][i].v, u);
            ans += 1LL * sz[G[u][i].v] * (n - sz[G[u][i].v]) * G[u][i].w;
        }
    }
    sz[u]++;
    return sz[u];
}
int main() {
    cin >> n >> m;
    init();
    for (int i = 0; i < m; i++) {
        cin >> g[i].u >> g[i].v >> g[i].w;
    }
    cout << kruskal() << " ";
    dfs(1, 0);
    cout << ans << endl;
    return 0;
}

基础换根

换根 指在无根树中由假设以 $u$ 为根算出的结果推导出以 $u$ 的某个子节点 $v$ 为根算出的结果的方法。常用于一次性求解一个算式在以每个节点为该无根树根时的值。

接下来我们来看这样一个问题。

#### [POI 2008] STA

给出一个 $n$ 个结点的树，找出一个结点为根，使得树上所有结点的深度之和最大。

解析

我们先假设 $1$ 号结点就是根结点，这时候，我们对树做一次 DFS 就可以求出每个点的子树的大小，并且同时也可以求出所有结点的深度之和。

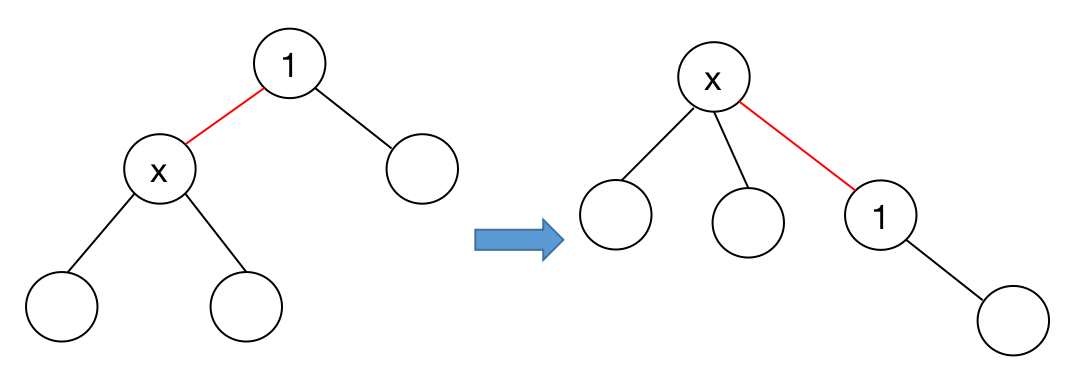
这时候，如果我们把根结点转移到 $1$ 号结点的一个儿子 $x$ 上，那么 $x$ 结点对应的所有以 $1$ 为根结点的子树中的结点的深度都要减去 $1$，而除了 $x$ 以外的其他儿子结点和 $1$ 结点的深度都要增加 $1$。所以对应总的深度和就可以计算出来。也就是说通过父结点信息我们可以推算出子结点的信息，这样我们就可以在树上进行动态规划了。

定义：

• $fa[u]$：表示整棵树以 $1$ 为根结点时，$u$ 的父结点；
• $size[u]$：表示整棵树以 $1$ 为根结点时，以 $u$ 为根的子树的结点数量；
• $f[u]$：表示整棵树以 $1$ 为根结点时，以 $u$ 为根的子树的所有结点的深度之和；
• $ans[u]$：表示整棵树以 $u$ 为根时所有结点的深度之和；

很容易想到递推式：$f[u]=\sum(f[v] + size[v])$，其中 $v$ 是 $u$ 的子结点 ，因为加上 $u$ 以后，$v$ 的所有子结点深度都会加 $1$，所以递推式里需要加上 $size[v]$；

我们用 $ans[u]$ 表示以 $u$ 为根时所有结点的深度之和，则对于根结点来说，$ans[u]=f[u]$，而对于非根结点 $u$ 的 $ans[u]$ 需要从父亲转移而来：\(\displaystyle ans[u] = ans[fa[u]] + n - 2\times size[u]\)

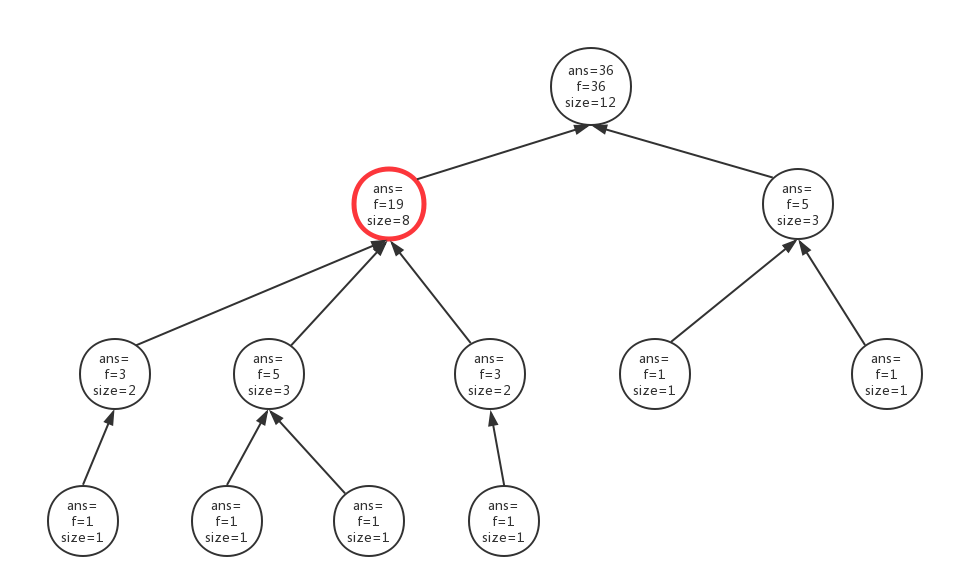
比如上面这个例子，我们自上而下计算到标红结点时，其父结点的 $ans$ 是 $36$，一共有 $12$ 个结点，因此有 $ans[u]=ans[fa[u]] + n - 2 \times size[u] = 36 + 12 - 2 \times 8 = 32$。

整个算法的流程如下：

1. DFS 一遍，由子结点信息得到 $size[x],f[x]$
2. 再 DFS 一遍，由父结点信息得到 $ans[x]$
3. 求出最大值

算法的整体时间复杂度 $\mathcal{O}(n)$。

区间动态规划

区间 DP

区间 DP：是指在一段区间上进行的一系列动态规划。

对于区间 DP 这一类问题，我们需要计算区间 $[1,n]$ 的答案，通常用一个二维数组 $dp$ 表示，其中 $dp[i][j]$ 表示区间 $[i,j]$ 的状态。

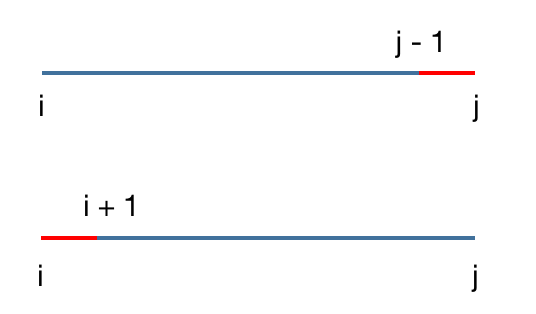
有些题目，$dp[i][j]$ 由 $dp[i][j-1]$ 与 $dp[i+1][j]$ 推得；

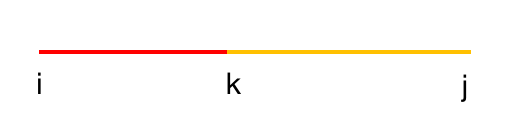
也有些题目，我们需要枚举区间 $[i,j]$ 内的中间点，由两个子问题合并得到，也可以说 $dp[i][j]$ 由 $dp[i][k]$ 与 $dp[k+1][j]$ 推得，其中 $l\leq k<r$。

对于长度为 $n$ 的区间 DP，我们可以先计算 $[1, 1], [2,2]\ldots [n,n]$ 的答案，再计算 $[1,2],[2,3]\ldots[n-1,n]$，以此类推，直到得到原问题的答案。

在写法上，往往是先枚举区间长度 $len$，再枚举区间的左端点 $i$，根据 $i$ 和 $len$ 推出右端点 $j = i + len - 1$，再进行状态转移。

代码模板如下：

for (int len = 2; len <= n; len++) {
    for (int i = 1; i + len - 1 <= n; i++) {
        int j = i + len - 1;
        // 转移
    }
}

别忘了初始化，就是在这段代码之前对 $dp[i][i]$ 进行赋值。

例题：[USACO06FEB] 奶牛的零食

题意

约翰经常给产奶量高的奶牛发特殊津贴，于是很快奶牛们拥有了大笔不知该怎么花的钱。为此，约翰购置了 $N$ 份美味的零食来卖给奶牛们。每天约翰售出一份零食。当然约翰希望这些零食全部售出后能得到最大的收益。这些零食有以下这些有趣的特性：

• 零食按照 $1\cdots N$ 编号，它们被排成一列放在一个很长的盒子里。盒子的两端都有开口，> 约翰每天可以从盒子的任一端取出最外面的一个。

• 这些零食储存得越久就越好吃。当然，这样约翰就可以把它们卖出更高的价钱。

• 每份零食的初始价值不一定相同．约翰进货时，第 $i$ 份零食的初始价值为 $V_i$。

• 第 $i$ 份零食如果在被买进后的第 $a$ 天出售，则它的售价是 $V_i \times a$。

约翰告诉了你所有零食的初始价值，并希望你能帮他计算一下，在这些零食全被卖出后，他最多能得到多少钱。

数据范围

$1 \leq N \leq 2000, 1 \leq V_i \leq 1000$

输入格式

第一行，一个正整数，表示 $N$。

接下来 $N$ 行，每行一个正整数，表示 $V_i$。

输出格式

一行，一个正整数表示答案。

样例输入

5
1
3
1
5
2

样例输出

43

解析

通过观察或手动模拟操作，我们可以发现每次操作完剩下的部分一定是一段连续区间，并且最后一次操作是把最后一个剩下的零食出售。

不妨设 $dp[i][j]$ 表示还剩下 $[i, j]$ 这些零食时后续最多还能得到多少钱。

初始化情况是 $dp[i][i] = V[i] \times N$ ，当只剩下最后一个零食时，一定是第 $N$ 天卖出它。

当剩余区间长度是 $len$ 时，即将卖出的是第 $N - len + 1$ 天的零食，如果卖第 $i$ 个零食，剩余区间为 $[i + 1, j]$，如果卖第 $j$ 个零食，剩余区间为 $[i, j - 1]$，那么状态转移方程为：

$dp[i][j] = \max(\textcolor{red}{dp[i + 1][j] + V[i]} \times (N - len + 1), \textcolor{red} {dp[i][j - 1] + V[j]} \times (N - len + 1))$

最后答案为 $dp[1][N]$

参考代码

#include <iostream>
#include <algorithm>
using namespace std;
int V[2005], dp[2005][2005];
int main() {
    int N;
    cin >> N;
    for (int i = 1; i <= N; i++) {
        cin >> V[i];
    }
    for (int i = 1; i <= N; i++)
    {
        dp[i][i] = V[i] * N;
    }
    for (int len = 2; len <= N; len++)
    {
        for(int i = 1; i + len - 1 <= N; i++)
        {
            int j = i + len - 1;
            dp[i][j] = max(dp[i + 1][j] + V[i] * (N - len + 1), dp[i][j-1] + V[j] * (N - len + 1));
        }
    }
    cout << dp[1][N] << endl;
    return 0;
}

例题：合并石子

题意

当前有 $N$ 堆石子，他们并列在一排上，每堆石子都有一定的数量。我们需要把这些石子合并成为一堆，每次合并都只能把 相邻 的两堆合并到一起，每一次合并的代价都是这两堆石子的数量之和，经过 $N-1$ 次合并后成为一堆。求把这些石子合并成一堆所需的最小代价。

数据范围

$1 \leq N \leq 100$

解析

这个题和以前学习优先队列时的《合并果子》不同的是每次必须选择 相邻 的两堆进行合并，所以不能使用《合并果子》的贪心策略了。

通过观察会发现每次合并都是把两个相邻的连续区间进行合并，比如第一次可以把 $[1,1]$ 和 $[2,2]$ 合并成 $[1,2]$ 。如果之前把 $[1, 2]$ 和 $[3, 4]$ 合并出来，接着可以把这两段再合并成 $[1, 4]$ 。

所以我们可以设 $dp[i][j]$ 表示合并了第 $i$ 堆石子到第 $j$ 堆石子所需的最小代价。

对于当前的最后一次合并操作，是把某两段合并成了 $[i, j]$，那么可以枚举两段中间的分界点 $k$，将 $[i, j]$ 拆成 $[i, k]$ 和 $[k + 1, j]$，表示是把这样的两段合并成一段的。

状态转移方程为：

$dp[i][j] = \min(dp[i][k] + dp[k+1][j] + (a[i] + … + a[j]))$

其中 $a[i] + … + a[j]$ 可以用前缀和优化一下，变为 $sum[j] - sum[i - 1]$ 。

状态转移方程为：

$dp[i][j] = \min(dp[i][k] + dp[k+1][j] + (sum[j] - sum[i - 1]))$

最后答案为 $dp[1][N]$，因为要枚举 $k$，所以时间复杂度是 $\mathcal{O}(n^3)$。

参考代码

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int inf = 0x3f3f3f3f;
int a[105], sum[105], dp[105][105];
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        sum[i] = sum[i - 1] + a[i];
    }
    for (int i = n; i >= 1; i--) {
        for (int  j = i + 1; j <= n; j++) {
            dp[i][j] = inf;
            for (int k = i; k < j; k++) {
                dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + (sum[j] - sum[i - 1]));
            }
        }
    }
    cout << dp[1][n] << endl;
    return 0;
}

破环成链

《石子合并》问题是把石子放成一排，如果石子放成一个环，第 $N$ 堆和第 $1$ 堆相邻，又该怎么做呢？

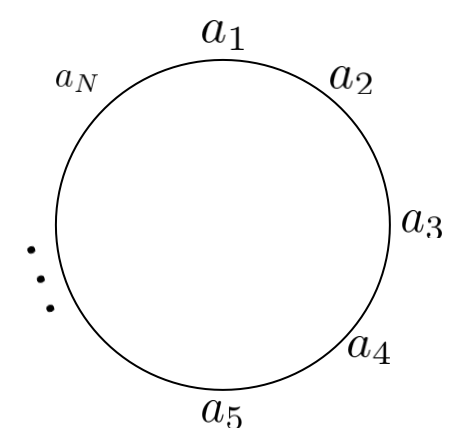
我们要想办法把它变成之前放成一排的问题，可以发现只要我们把

• $a_1, a_2, a_3, \cdots, a_N$
• $a_2, a_3, a_4, \cdots, a_N, a_1$
• $a_3, a_4, a_5, \cdots, a_N, a_1, a_2$
• …
• $a_N, a_1, a_2,\cdots, a_{N - 1}$

这 $N$ 种放成一排的情况都考虑清楚，取其中的最优解，就一定是放成环的样子的最优解。

但如果做 $N$ 次区间 DP 时间复杂度就变成了 $\mathcal{O}(n^4)$，并且我们可以发现在其中有一些状态是重复计算的。

有一种很常用的方法可以避免这样的重复计算，就是把数组复制一遍，把复制的放在原数组的后边，形成一个新的序列 $b$，其中的元素是：

$a_1, a_2, a_3, \cdots, a_N, a_1, a_2, a_3, \cdots, a_N$

此时，

• $a_1, a_2, a_3, \cdots, a_N$
• $a_2, a_3, a_4, \cdots, a_N, a_1$
• $a_3, a_4, a_5, \cdots, a_N, a_1, a_2$
• …
• $a_N, a_1, a_2,\cdots, a_{N - 1}$

这里的每一种情况后对应成了复制完成后数组的一段连续区间。

• $a_1, a_2, a_3, \cdots, a_N$ 是区间 $b_1\sim b_N$
• $a_2, a_3, a_4, \cdots, a_N, a_1$ 是区间 $b_2\sim b_{N+1}$
• $a_3, a_4, a_5, \cdots, a_N, a_1, a_2$ 是区间 $b_3\sim b_{N+2}$
• …
• $a_N, a_1, a_2,\cdots, a_{N - 1}$ 是区间 $b_N\sim b_{2\times N-1}$

所以我们只需要正常做区间 DP ，最后求 $dp[1][N], dp[2][N + 1], …, dp[N, 2 \times N - 1]$ 的最大值即可。

区间 DP 记录路径

在以前我们解决动态规划类问题的时候，都可以通过把转移点记在一个数组 $pre$ 里并从结尾倒推的方式找到决策的路径，找到选择的方案。

对于区间 DP，我们也可以记录路径，还是利用一个数组记录转移点。

如果 $dp[i][j]$ 是从 $dp[i - 1][j], dp[i][j - 1]$ 或者 $dp[i - 1][j - 1]$ 转移过来的，那么可以跟之前一样，用循环倒推回去，只不过这里需要用两个变量表示目前推到的 $i, j$ 。

但是如果 $dp[i][j]$ 是从 $dp[i][k]$ 和 $dp[k + 1][j]$ 转移的呢？

此时正确的操作顺序是先完成区间 $[i, k]$ 和区间 $[k + 1][j]$ 的操作，再进行这一次的合并。这个过程很像递归回溯，也很像二叉树的后序遍历，所以我们用递归的方式来找到路径。

代码模板如下：

void solve(int i, int j) {
    if (i == j) {
        return;
    }
    solve(i, pre[i][j]);
    solve(pre[i][j] + 1, j);
    cout << i << " " << pre[i][j] << " " << k << endl;
}

例题：[NOIP 2003] 加分二叉树

题意

设一个 $n$ 个节点的二叉树 tree 的中序遍历为 $(1,2,3,\cdots,n)$，其中数字 $1,2,3,\cdots,n$ 为节点编号。每个节点都有一个分数（均为正整数），记第 $i$ 个节点的分数为 $d_i$，tree 及它的每个子树都有一个加分，任一棵子树 subtree（也包含 tree 本身）的加分计算方法如下：

subtree 的左子树的加分 $\times$ subtree 的右子树的加分 $+$ subtree 的根的分数。

若某个子树为空，规定其加分为 $1$，叶子的加分就是叶节点本身的分数。不考虑它的空子树。试求一棵符合中序遍历为（$1,2,3,\cdots,n$）且加分最高的二叉树 tree。

要求输出：

（1）tree 的最高加分

（2）tree 的前序遍历

输入格式

第 $1$ 行：一个整数 $n$（$n<30$），为节点个数。

第 $2$ 行：$n$ 个用空格隔开的整数，为每个节点的分数（分数 $<100$）。

输出格式

第 $1$ 行：一个整数，为最高加分（结果不会超过 $4,000,000,000$）。

第 $2$ 行：$n$ 个用空格隔开的整数，为该树的前序遍历。

样例输入

5
5 7 1 2 10

样例输出

145
3 1 2 4 5

解析

对于中序遍历，任何一个节点的左子树是序列的一段连续区间，右子树也是序列的一段连续区间。

如果我们从下往上考虑整棵树，这是一个把两段区间（两棵子树）合并成一个区间（一棵子树）的过程。

首先考虑第一问。

可以设 $dp[i][j]$ 表示把 $[i, j]$ 合并为一棵子树的最高加分，枚举根节点 $k$ 进行转移。

其中 $k = i$ 或者 $k = j$ 是该子树的根节点只有一边子树的情况，两种情况的结果分别是 $dp[i + 1][j] + d[i]$ 和 $dp[i][j - 1] + d[j]$ 。

对于一般的 $i < k < j$ 的情况，结果是 $dp[i][k - 1] \times dp[k + 1][j] + d[k]$ 。

转移时取所有结果的最大值。

第一问的答案为 $dp[1][n]$ ，注意最开始初始化 $dp[i][i] = d[i]$ 。

对于第二问，我们想构建出这棵二叉树，只需要在 DP 的过程中记录选择的根的情况，输出时从区间 $[1, n]$ 出发，按照前序遍历，应该先输出选择的根，再分别递归进入左子区间和右子区间。>

注意没有左子区间和右子区间的特殊情况。

参考代码

#include <iostream>
using namespace std;
int d[35], pre[35][35];
long long dp[35][35];
void solve(int i, int j) {
    if (i == j)
    {
        cout << i << " ";
        return;
    }
    cout << pre[i][j] << " ";
    if (pre[i][j] != i) {
        solve(i, pre[i][j] - 1);
    }
    if (pre[i][j] != j) {
        solve(pre[i][j] + 1, j);
    }
}
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> d[i];
    }
    for (int i = 1; i <= n; i++) {
        dp[i][i] = d[i];
    }
    for (int len = 2; len <= n; len++) {
        for (int i = 1; i + len - 1 <= n; i++) {
            int j = i + len - 1;
            if (dp[i + 1][j] + d[i] > dp[i][j]) {
                dp[i][j] = dp[i + 1][j] + d[i];
                pre[i][j] = i;
            }
            if(dp[i][j-1] + d[j] > dp[i][j]) {
                dp[i][j] = dp[i][j-1] + d[j];
                pre[i][j] = j;
            }
            for (int k = i + 1; k <= j - 1; k++) {
                if(dp[i][k-1] * dp[k+1][j] + d[k] > dp[i][j]) {
                    dp[i][j] = dp[i][k-1] * dp[k+1][j] + d[k];
                    pre[i][j] = k;
                }
            }
        }
    }
    cout << dp[1][n] << endl;
    solve(1, n);
    return 0;
}

算法的数据结构优化

双端队列

双端队列：deque，即：可以在两端进行插入、弹出、删除等操作的队列。

deque与vector非常相似，不仅可以在尾部插入和删除元素，还可以在头部插入和删除。不过当考虑到容器元素的内存分配策略和操作性能时，deque相对vector较为有优势。

在 C++ 中，双端队列被写在头文件#include<deque>中。

下面我们来讲一下，双端队列的常用方法函数：

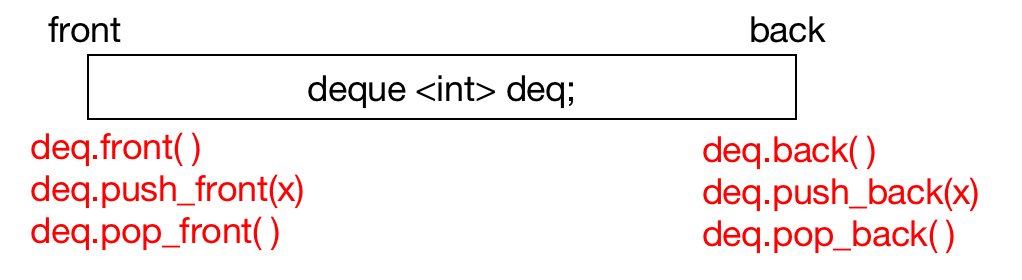
• deq.front()：返回双向队列的头部元素。
• deq.push_front(x)：把元素 $x$ 插入到双向队列的头部。
• deq.pop_front()：弹出双向队列的第一个元素。
• deq.back()：返回双向队列的尾部元素。
• deq.push_back(x)：把元素 $x$ 插入到双向队列的尾部。
• deq.pop_back()：弹出双向队列的尾部元素。
• deq.empty()：查看是否为空队列，是的话返回true，不是返回false。
• deq.clear()：清除队列里的所有数据。
• deq.size()：输出现有元素的个数。

下面让我们看一下双端队列的使用。

deque<int> deq;

//两种入队列方式
deq.push_back(1);    //尾部插入元素
deq.push_back(2);
deq.push_front(3);   //头部插入元素

//三种访问方式
cout << deq[0] << endl;       //按照下标访问元素，3
cout << deq.front() << endl;  //返回头元素的值，3
cout << deq.back() << endl;   //返回尾元素的值，2

//两种出队方式
deq.pop_front();   //头部出队
deq.pop_back();    //尾部出队

//遍历队列中的元素
while (!deq.empty()) {
    cout << deq.front() << endl;  //此时队列中只有元素 1
    deq.pop_front();
}

01 BFS

以前学习广度优先搜索的时候，经常用广度优先搜索解决迷宫或图中的最短路问题，只要边权都是 $1$ 就可以用 BFS 解决。

那如果是01 图（边权是 $1$ 或 $0$ ）呢，换句话说迷宫或者图中有些路是不耗时间可以瞬移经过的，此时又可以有什么巧妙的方法求解最短路呢？

回想 BFS 的过程，关注队列里的情况。在 BFS 的队列里，队首和队尾步数最多差 $1$，整个队列分为两部分，前一部分是这一层还没有被取出的点，后一部分是下一层已经被放进来的点。

如果边权只有 $1$，我们很显然就是把新点放到队尾，如果边权有 $0$，其实我们只需要把它当作当前层的点，放到队首就可以了。

这样在搜索的过程中队列里依然是前一部分是当前层，后一部分是下一层这样的情况，就可以用 $\mathcal{O}(n)$ 的时间复杂度计算最短路了。

不过在写代码的时候还需要注意，只有当这一次到达该点的距离更小时才将其放入队列，并且如果取出的时候从起点到该点的距离已经发生改变，需要将该点直接出队。

其实很简单，我们的需求是在某个点 $x$ 从队首被取出的时候，需要满足起点到该点的距离最短。

在之前学习的不带权图广搜当中，点 $x$ 第一次进队的时候，此时记录的从起点到 $x$ 的路径长度就一定是最短的了。

但是在这个问题里中，点 $x$ 第一次进队的时候，就不一定代表找到起点到 $x$ 的最短路了。

举一个例子：

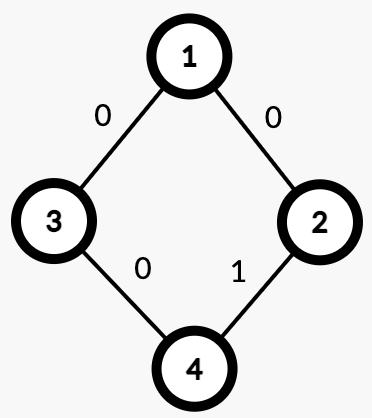
我们从 $1$ 号节点出发，将 $2,3$ 先后入列。这种情况下，我们是扫描到 $2$ 到 $4$ 的边将其第一次入列的，此时最短路径长度是 $1$，但是我们知道从 $1,3,4$ 这条路径走，路径长度是 $0$。

电路维修

下面我们来看一道题目：

达达是来自异世界的魔女，她在漫无目的地四处漂流的时候，遇到了善良的少女翰翰，从而被收留在地球上。

翰翰的家里有一辆飞行车。有一天飞行车的电路板突然出现了故障，导致无法启动。电路板的整体结构是一个 $R$ 行 $C$ 列的网格 $(R,C\le 500)$，如下图所示。

每个格点都是电线的接点，每个格子都包含一个电子元件。

电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。在旋转之后，它就可以连接另一条对角线的两个接点。

电路板左上角的接点接入直流电源，右下角的接点接入飞行车的发动装置。

达达发现因为某些元件的方向不小心发生了改变，电路板可能处于断路的状态。她准备通过计算，旋转最少数量的元件，使电源与发动装置通过若干条短缆相连。

不过，电路的规模实在是太大了，达达并不擅长编程，希望你能够帮她解决这个问题。注意：只能走斜向的线段，水平和竖直线段不能走。

输入格式

对于每组数据，第一行包含正整数 $R$ 和 $C$，表示电路板的行数和列数。

之后 $R$ 行，每行 $C$ 个字符，字符是/和\中的一个，表示标准件的方向。

输出格式

输出一个正整数，表示所需的缩小旋转次数。

如果无论怎样都不能使得电源和发动机之间连通，输出 NO SOLUTION。

我们先看一组样例：

3 5
\/\
\///
/\\

其实也就是：

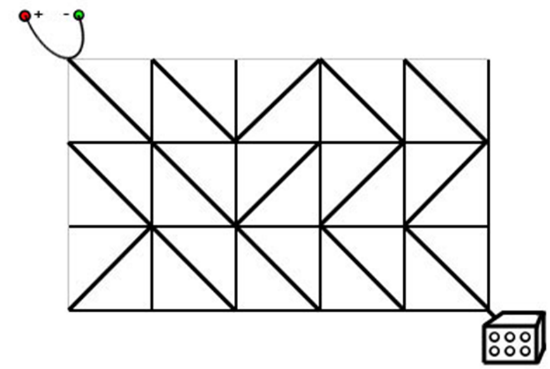
这个图片，他的答案是 $1$，如下图：

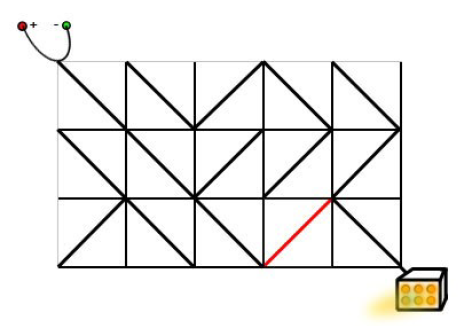
只需要改变一条边，即可联通电路。

了解了题目之后，我们发现，这是一道图有关的题目，那么如何才能和我们熟悉的图结合在一起并建立图模型呢？

我们发现，题目中边只有两种属性，一种是\，一种是/，而且两种属性可以互换，求最小的互换次数。

我们可以从“只有两种属性，可以互换”这个点出发，将图构建为01图。

这里假设，当前我们到达 $mp_{i,j}$ 这个点，并且此时边的属性是\，那么就意味着 $mp_{i,j}$ 可以不需要改变就能到达 $mp_{i+1,j+1}$ 这个点，即：$mp_{i,j}$ 与 $mp_{i+1,j+1}$ 的边权值为 $0$。而如果需要将这条边进行反转，也就是说，$mp_{i,j+1}$ 到达 $mp_{i+1,j}$ 的边权值为 $1$。

接下来，我们可以通过双端队列进行 01 BFS。算法的整体框架与一般的广搜类似，只是在每个节点沿分支拓展时稍作改变。如果这条分支边权为 $0$，则从队首入队，否则从队尾入队。这样我们能保证，任意时刻广搜队列中节点对应的距离值都有“两端性”和“单调性” ，每个节点第一次被访问时，就能得到从左上角到该节点的最短距离。

下面我们证明一下这个算法的正确性：

由于我们最终目标是求路径权值和，而权值为 $0$ 的边无论走多少条权值和依旧是 $+0$，因此我们可以优先走权值为 $0$ 的边，更新与这些边相连的点 $x$ 的 $d_x$（$d_i$ 为从 $s$ 到 $i$ 最小权值和），此时 $d_x$ 一定是最小的，因为它是由尽可能多的权值为 $0$ 的边更新而来。所以在队列中取出的节点同时满足“连通性”和“权值最小” ，因此每个节点仅需被更新一次。

我们进行图的构造，这里我们的构造方式有些不同，我们将每个点位，按从左到右，从上到下依次标号，其中：$(0,0)$ 的标号为 $1$。

因为每行有 $c+1$ 个点，设 $c = c + 1$。

对于第 $i(0 \leq i <r)$ 行第 $j(1 \leq i < c)$ 个字符：

1. $i\times c + j$ 为左上角点位。
2. $i\times c + j + 1$ 为右上角点位。
3. $(i + 1)\times c + j$ 为左下角点位。
4. $(i+1)\times c+j+1$ 为右下角点位。

所以图中起点为 $1$，终点为 $(r + 1) \times c$。

c++;
char str[MAXN];
for (int i = 0; i < r; i++) {
    scanf("%s", str);
    for (int j = 1; j < c; j++) {
        if (str[j - 1] == '\') {
            addEdge(i * c + j, (i + 1) * c + j + 1, 0);
            addEdge((i + 1) * c + j + 1, i * c + j, 0);
            addEdge((i + 1) * c + j, i * c + j + 1, 1);
            addEdge(i * c + j + 1, (i + 1) * c + j, 1);
        } else {
            addEdge(i * c + j, (i + 1) * c + j + 1, 1);
            addEdge((i + 1) * c + j + 1, i * c + j, 1);
            addEdge((i + 1) * c + j, i * c + j + 1, 0);
            addEdge(i * c + j + 1, (i + 1) * c + j, 0);
        }
    }
}

接下来，我们看看如何进行双端队列bfs，模拟刚刚讲过的算法：

int d[MAXN];
bool vis[MAXN];
void solve() {
    memset(d, 0x3f, sizeof(d));
    memset(vis, false, sizeof(vis));
    d[1] = 0;
    deque<int> q;
    q.push_back(1);
    while (!q.empty()) {
        int x = q.front();
        q.pop_front();
        if (vis[x]) {
            continue; // 当某个点再次被遍历时，我们已经获得了到达它的最小值，所以直接 continue。
        }
        vis[x] = true;
        for (int i = head[x]; i; i = Next[i]) {
            int y = ver[i], z = edge[i];
            d[y] = min(d[x] + z, d[y]);
            if(z) {
                q.push_back(y); // 边权为 1 的点放到队尾。
            } else {
                q.push_front(y); // 边权为 0 的点放到队首。
            }
        }
    }
}

和普通队列的区别在于，我们需要对边权大小进行判断，从而决定新加的点是加在队首还是队尾。

在代码内还有一个比较大的区别在于：

int y = ver[i], z = edge[i];
d[y] = min(d[x] + z, d[y]);
if(z) {
    q.push_back(y); // 边权为 1 的点放到队尾。
} else {
    q.push_front(y); // 边权为 0 的点放到队首。
}

中途相遇法

中途相遇法常被称作 Meet-in-the-Middle ，可以看成是搜索算法的一个改进，一般来说用于深搜（DFS）和广搜（BFS）。

我们首先假象一个搜索场景：

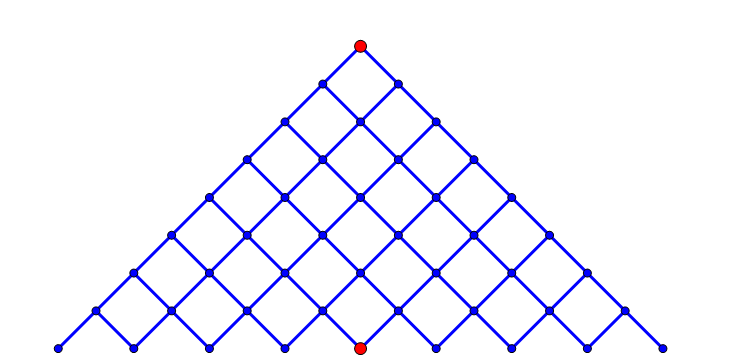
假设从上面的红点开始进行搜索，找一条能通向下面那个红点的路径，每个点都有两条岔路可供选择。

显然如果我们简单的从上面那个点开始 BFS 或 DFS，代价是较大的，在最差的情况下，可能需要把整张图的所有从上到下的路径给走一遍。

当然把搜索的重任全部交给一个节点是不合理的。于是 Meet-in-the-Middle 算法就诞生了。顾名思义，就是两个节点各自向中间搜索，直至碰头。

我们接下来用数学来具体推导一下这种搜索方案的复杂度。

假设向外搜索 $n$ 层需要的代价为 $f(n)$。如果不用 Meet-in-the-Middle 那么复杂度当然是 $\mathcal{O}(f(n))$。

如果使用了 Meet-in-the-Middle，那么从起点开始需要搜索的代价为 $f(\frac{n}{2})$，从终点开始搜索的代价也是 $f(\frac{n}{2})$，总代价就是 $2\times f(\frac{n}{2})$，复杂度为 $\mathcal{O}(f(\frac{n}{2}))$。

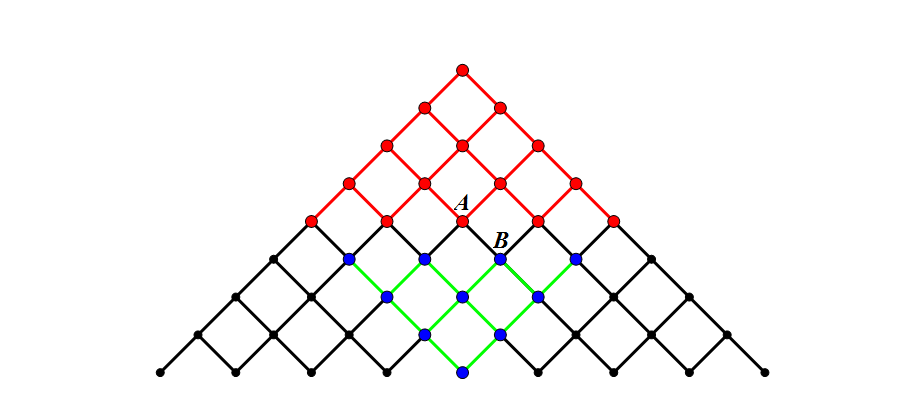
在上图中红点的部分为起点开始向外搜索到的点，而蓝点表示从终点开始搜索到的点。假如此时搜索进行到点 B，直接就能发现 A 点是从起点过来的点，那么也就自然找到了一条从起点 $\rightarrow A\rightarrow B \rightarrow$ 终点 的路径，然而我们发现，整个图里面黑色部分的节点与边其实我们都可以不用访问。当整张图扩大时，这种优化的效果还是比较明显的。

当然从这个搜索模型来看，无论是不是使用 Meet-in-the-Middle 复杂度均为 $\mathcal{O}(n^2)$。但是当 $f(n)$ 为指数函数时该算法的效果就会非常明显。比如 $f(n)=2^n$，那么不用 Meet-in-the-Middle 复杂度即为 $\mathcal{O}(2^n)$，但是使用了 Meet-in-the-Middle 的复杂的只有 $\mathcal{O}(2^{\frac{n}{2}})$，相当于直接开了一个根号。Meet-in-the-Middle 算法也有一定的局限性，首先是要求搜索图中的节点状态转移都是可逆的，即如果 A 点能到 B 点，B 点也能一下子回到 A 点，否则就不存在从终点出发这个说法了。其次是需要额外的数据结构存储找过的节点，一般来说用数组，set 或者 map。

例题：[CEOI 2015] 冰球世锦赛

题意

这一年世界冰球锦标赛在捷克举行， Bobek 来到了布拉格，他想要观看一些比赛。他对球队没有偏好，可用时间上也没有限制，甚至如果他有无限的钱，他愿意观看所有比赛，但是他的钱是有限的，不过他可以把他拥有的所有钱用在买票上。

现在你知道了每一场比赛对应的票价，你能帮他算算有多少种观看比赛的方案满足选择的比赛的总票价不会超过 Bobek 所拥有的钱吗？

两种方案不同当前仅当存在至少一场比赛在一种方案被选择而在另一种方案中没有被选择。

输入格式

第一行包含两个正整数 $N, M(1 \leq N \leq 40, 1 \leq M \leq 10 ^ {18})$ ，分别表示比赛场数和 Bobek 所拥有的钱。

第二行包含 $N$ 个正整数，分别表示每一场比赛的票价，一场比赛的票价不超过 $10 ^ {16}$

输出格式

输出一行，包含一个整数，表示 Bobek 可以选择观看比赛的方案数。注意数据范围，这个数不会超过 $2 ^ {40}$ 。

样例输入

5 1000
100 1500 500 500 1000

样例输出

8

样例解释

可行的 $8$ 种方案如下：

• 不观看比赛
• 观看第 $1$ 场比赛
• 观看第 $3$ 场比赛
• 观看第 $4$ 场比赛
• 观看第 $1$ 场和第 $3$ 场比赛
• 观看第 $1$ 场和第 $4$ 场比赛
• 观看第 $3$ 场和第 $4$ 场比赛
• 观看第 $5$ 场比赛

解析

把比赛分成前一半和后一半，分别搜索枚举出所有总金额不超过 $M$ 的方案，合并时对于前一半的每种方案 $a$，在后一半的方案中二分出最小的超过 $M$ 减前一半所选方案 $b$，后一半的方案中 $b$ 前边的方案都是可以和 $a$ 搭配出整个的选择方案的，求和即可。

参考代码

#include <iostream>
#include <algorithm>
using namespace std;
long long price[45];
long long ans1[2000005], ans2[2000005];
long long ans;
int cnt1, cnt2;
int N;
long long M;
/*
price 价格数组
N 本次搜索的总场数
ans 存储合法情况的数组
cnt 表示合法情况数
p 表示当前在考虑的场次
now 表示当前选择的总票价
*/
void dfs(long long *price, int N, long long *ans, int &cnt, int p, long long now) {
    if (p == N)
    {
        ans[cnt++] = now;
        return;
    }
    dfs(price, N, ans, cnt, p + 1, now);
    if (now + price[p] <= M)
    {
        dfs(price, N, ans, cnt, p + 1, now + price[p]);
    }
}
int main() {
    cin >> N >> M;
    for (int i = 0; i < N; i++) {
        cin >> price[i];
    }
    dfs(price, N / 2, ans1, cnt1, 0, 0);
    dfs(price + N / 2, N - N / 2, ans2, cnt2, 0, 0);
    sort(ans1, ans1 + cnt1);
    sort(ans2, ans2 + cnt2);
    for (int i = 0; i < cnt1; i++)
    {
        ans += upper_bound(ans2, ans2 + cnt2, M - ans1[i]) - ans2;
    }
    cout << ans << endl;
    return 0;
}

记忆化搜索与 DAG 上的动态规划

斐波那契数列

斐波那契数列：

\[\displaystyle f_n = \begin{cases}1 & n=1,2\\ f_{n-1}+f_{n-2} & n\ge 3 \end{cases}\]

我们都知道可以用 递推 的方式，来求出斐波那契数列的第 $n$ 项。

但是在这一节，我们尝试用 DFS 的方式来计算斐波那契数列的第 $n$ 项。

我们先来看一个普通的 DFS

int dfs(int n) {
    if(n == 1 || n == 2) {
        return 1;
    }
    return dfs(n - 1) + dfs(n - 2);
}

我们知道这份代码效率很低，因为会发生大量的重复计算。

例如我们计算:dfs(6)时，会递归计算dfs(5)与dfs(4)，其中计算dfs(5)时又会递归计算dfs(4)与dfs(3)。于是dfs(4)就被计算了两次。

而且在计算dfs(4)时也会进行递归，其递归计算的状态也都会被重复计算。并且dfs(n)中的 $n$ 越大，重复计算的情况就越多，从而导致效率很低。

记忆化搜索

现在我们想办法提高 DFS 的效率：DFS 效率底下是由于出现了大量的重复计算，所以我们从避免重复计算的方向来进行优化。

记忆化搜索 可以通过记录每次的计算结果来避免重复计算，这样可以使得每一种状态只被计算一次，极大程度上提升了效率。

[NOIP2005] 采药

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药（共 $m$ 株），采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

现在已知山洞中共有 $n$ 株草药，采第 $i$ 株采药需要花费 $t[i]$ 时间，可以获得 $c[i]$ 价值。

采药的时间 $T (1 \le T \le 1000)$ ，一共有不超过 $100$ 个草药，每个草药的价值和消耗的时间不超过 $100$ 。

我们可以看出这是一道 01 背包 的裸题，可以设 $f[j]$ 表示消耗时间为 $j$ 时可以获得的最大价值和，然后进行通过递推进行转移：

for (int i = 1; i <= n; i++) {
    for (int j = T; j >= t[i]; j--) {
        f[j] = max(f[j], f[j - t[i]] + c[i]);
    }
}
cout << f[T] << endl;

实际上我们还可以通过dfs求解小数据时的答案。设void dfs(int x, int sumt, int sumc)表示在前 $1\sim (x- 1)$ 株药草中，已经花费了 $sumt$ 的时间，采了 $sumc$ 价值的药。

int n, T, ans = 0;
void dfs(int x, int sumt, int sumc) {
    ans = max(ans, sumc);
    if (x > n || sumt == T) {
        return;
    }
    if (sumt + t[x] <= T) {
        dfs(x + 1, sumt + t[x], sumc + c[x]);
    }
    dfs(x + 1, sumt, sumc);
}

dfs(1, 0, 0);

我们尝试用记忆化搜索的方式来求解这个动态规划方程。

我们设状态 $f[i][j]$ 表示在 $i,i+1,\cdots,n-1, n$ 中选择物品，剩余时间为 $j$ 时能选出的最大价值和。

然后 DFS 时每次枚举某一个物品选择或者不选，当某些状态已经得到答案时，可以直接返回结果。

int f[110][1010];
int dfs(int i, int T){
    if (i == n + 1) {
        return 0;
    }
    if (f[i][T] != -1) {
        return f[i][T];
    }
    int &r = f[i][T];
    r = dfs(i + 1, T);
    if (t[i] <= T) {
        r = max(r, dfs(i + 1, T - t[i]) + c[i]);
    }
    return r;
}

理解记忆化搜索与动态规划

前一个问题是很经典的 0/1 背包问题，我们之前学过如何用动态规划来求解这个问题。动态规划提升计算效率的原理就是通过记录子问题的答案，在求解更大规模问题时使用子问题的答案计算当前问题。

仔细分析记忆化搜索的过程，我们在记忆化搜索时也会设计状态，记录每一个子问题的答案。

我们可以将记忆化搜索视为一种实现动态规划的方式。但是与递推相比，记忆化搜索的方式可能会产生额外的空间开销以及常数级时间开销。

• 额外的空间开销：记忆化搜索需要记录所有的状态，但是递推方式求解动态规划无需记录所有状态，可以只保留会对后续状态造成影响的状态。例如这次的背包问题，递推做法可以将空间复杂度优化到 $\mathcal{O}(T)$ ，但是在记忆化搜索中我们需要记录所有的状态，空间复杂度为 $\mathcal{O}(MT)$ 。
• 额外的常数时间开销：递归是常数开销很大的一种操作，在记忆化搜索中，每一种状态都可能产生大量递归，这取决于方程转移的路径条数。相比于递推计算时迭代产生的常数时间开销，递归产生的常数时间开销要大得多。

既然使用记忆化搜索会导致时间上、空间上都劣于递推，那么记忆化搜索有什么存在必要呢？

观察记忆化搜索的过程，我们发现：记忆化搜索无需考虑枚举顺序（而递推是需要严格考虑枚举顺序的），我们会判断每一个状态是否被计算过，如果该状态没有被计算过则进行递归计算。所以在一些计算顺序比较复杂的动态规划中，记忆化搜索就是一个不错的选择，例如 在 DAG 上 dp，复杂的 区间类 dp 等等。

记忆化搜索实现区间DP

之前我们已经学习过区间 DP。

如果区间 $[i,j]$ 的贡献 $dp[i][j]$ 是通过 $dp[i][k]$ 与 $dp[k+1][j]$ (其中 $i\leq k < j$)计算出来的。

那么就需要先计算出区间 $[i,k]$ 与 区间 $[k+1,j]$ 的贡献。也就是说一个大的区间贡献是通过它的两个互补子区间计算而来的，符合分治思想。我们可以使用记忆化搜索，先计算出子区间的贡献，回溯的时候进行区间贡献的合并。

例题《沙子合并》

设有 $N$ 堆沙子排成一排，其编号为 $1,2,3,\cdots,N$。每堆沙子有一定的数量，可以用一个整数来描述，现在要将这 $N$ 堆沙子合并成为一堆，每次只能合并相邻的两堆，合并的代价为这两堆沙子的数量之和，合并后与这两堆沙子相邻的沙子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同。

如有 $4$ 堆沙子分别为 $1,3,5,2$ 我们可以先合并 $1$、$2$ 堆，代价为 $4$，得到 $4,5,2$ 又合并 $1,2$ 堆，代价为 $9$，得到 $9,2$，再合并得到 $11$，总代价为 $4+9+11=24$，如果第二步是先合并 $2,3$ 堆，则代价为 $7$，得到 $4 7$，最后一次合并代价为 $11$，总代价为 $4+7+11=22$；问题是：找出一种合理的方法，使总的代价最小。输出最小代价。

输入格式

第一行一个数 $N(1\leq N \leq 300)$ 表示沙子的堆数 $N$。

第二行 $N$ 个数 $a_i(1\leq a_i \leq 100)$，表示每堆沙子的质量。

输出格式

合并的最小代价。

样例输入

4
1 3 5 2

样例输出

22

题意：$n$ 堆沙子，每次可以将相邻的两堆沙子合并为一堆新的沙子，代价为这两堆沙子的和，将所有沙堆合并为一堆后的最小代价。

设 $dp[l][r]$ 表示的是将区间 $[l,r]$ 合并为一堆沙子的最小花费，想要将区间 $[l,r]$ 合并为一堆沙子，需要在这个区间内枚举一个点 $k(l\leq k < r)$，点 $k$ 将区间分为两部分 $[l,k], [k+1,r]$，表示的是两堆沙子。

如果已经计算出得到这两堆沙子的代价： $dp[l][k]$ 和 $dp[k+1][r]$，就可以将这两个区间（两堆沙子）进行合并，合并两堆沙子的代价：$dp[l][k] + dp[k+1][r] + \text{这两堆沙子的数量和}$。（其中这两堆沙子的数量和为：沙子区间 $[l,r]$ 的数量和，所以可以使用前缀和求解）。

因为将大区间分为小区间进行求解符合分治思想，所以我们可以使用记忆化搜素求解 $dp[l][r]$ 的值。

如果用：

• a[i] 表示第 $i$ 堆沙子的数量。
• sum[i] 表示前 $i$ 堆沙子的数量和。
• inf = 0x3f3f3f3f 表示一个特别大的数。
• dp[l][r] 表示将区间 $[l,r]$ 合并为一堆沙子的最小花费。

核心代码展示

for (int i = 1; i <= n; i++) { //求解前缀和
    sum[i] = sum[i-1] + a[i];
}

memset(dp, inf, sizeof(dp)); // 初始化为无穷大

int dfs(int l, int r) {
    if (l == r) return dp[l][r] = 0; // 只有一堆沙子，合并的代价为 0
    if (dp[l][r] != inf) return dp[l][r]; // 该区间已经合并过了，直接返回值
    for (int k = l; k < r; k++) { // 枚举分割点 k，将区间分为两部分：[l,k], [k+1, r]
        int val = dfs(l, k) + dfs(k + 1, r) + (sum[r] - sum[l-1]);
        dp[l][r] = min(dp[l][r], val);
    }
    return dp[l][r];
}

DAG 上 DP

[HAOI2016] 食物链

给定 $n$ 个物种和 $m$ 条能量流动关系，求其中的食物链条数。物种的名称从 $1$ 到 $n$ 编号， $M$ 条能量流动关系形如 $a_1 \to b_1,a_2\to b_2,a_3\to b_3 \cdots a_{m-1}\to b_{m-1}, a_m\to b_m$ 其中 $a_i\to b_i$ 表示能量从物种 $a_i$ 流向物种 $b_i$ ,注意单独的一种孤立生物不算一条食物链。

食物链：如果从 $x$ 到 $y$ 的某条路径是沿着能量流动方向移动的，并且 $x$ 没有入边, $y$ 没有> 出边，则该条路径为一条食物链。

题目保证不会出现重复的能量流动关系，并且能量不会环形流动。

显然，题中所给的的是 DAG ，即有向无环图。我们要做的就是统计这个 DAG 中有多少条不同路径 $(u,v)$ 满足 $u$ 没有入边, $v$ 没有出边。注意相同起点与终点之间可能有多条路径。

我们可以考虑使用动态规划来解决这个问题： 设 $f[u]$ 表示从没有入边的点到达点 $u$ 有多少条不同的路径。

• 所有没有入边的点的 $f$ 值应该初始化为 $1$
• 转移方程为： $f_v = \sum_{(u,v)\in E}f_u$
• 答案计算为： $ans = \sum_{out_u = 0 \text{且} in_u \neq 0}f_u$ ，其中 $out_u$ 为点 $u$ 的出度, $in_u$ 为点 $u$ 的入度

实现这个动态规划有两种方法：记忆化搜索与拓扑排序。

记忆化搜索解决 DAG 上 DP

我们观察转移方程： $f[v] = \sum_{(u,v)\in E}f[u]$

所以在计算一个点时，我们需要递归计算其所有入边，并且将对应点的 $f$ 值累加到该点的 $f$ 值中。所以可以考虑反向建边，这样我们就可以直接通过边表得知一个点应该由哪些点的 $f$ 值来更新。

相应的，由于我们反向建边，最终贡献答案的点需要满足的条件变为：入度为 $0$ ，并且有出边（如果入度为 $0$ 且没有出边，则该点是一个单独的点）。

参考代码

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 100010; // 点数量
const int maxm = 200010; // 边数量
struct Edge { // 邻接表相关
    int to, next;
} G[maxm];
int head[maxn], cnt, deg[maxn]; // deg 为入度

void addEdge(int u, int v) {
    G[++cnt].to = v;
    G[cnt].next = head[u];
    head[u] = cnt;
    ++deg[v]; // 统计入度
}
int f[maxn];
int dfs(int u) {
    if(!head[u]) return 1;
    if(f[u] != -1) return f[u];
    f[u] = 0;
    for(int i = head[u];i;i=G[i].next) {
        int v = G[i].to;
        f[u] += dfs(v);
    }
    return f[u];
}
int main(){
    int n, m;
    scanf("%d%d", &n, &m);
    int u, v;
    for (int i = 1; i <= m; ++i) {
        scanf("%d%d", &u, &v);
        addEdge(v, u); // 反向建边
    }
    int ans = 0;
    memset(f, -1, sizeof(f));
    for (int i = 1; i <= n; i++) {
        if(deg[i] == 0 && head[i]) ans += dfs(i);
    }
    printf("%d\n",ans);
    return 0;
}

拓扑排序解决 DAG 上 DP

我们可以在这里应用拓扑排序算法来求出拓扑序，然后让方程按照拓扑序进行转移。

与记忆化搜索的把大状态分割为小状态不同，我们使用拓扑序进行转移时采取的方式是将小状态的答案贡献到大状态中。即我们枚举到拓扑序的某一个点 $u$ 时， $f[u]$ 已经计算完成，我们需要枚举由该点出发的所有边 $(u,v)$ , 然后将 $f[u]$ 的值贡献到 $f[v]$ 中，即 f[v] += f[u]。

参考代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;
const int maxn = 100010; // 点数量
const int maxm = 200010; // 边数量
struct Edge { // 邻接表相关
    int to, next;
} G[maxm];
int head[maxn], cnt, deg[maxn]; // deg 为入度

void addEdge(int u, int v) {
    G[++cnt].to = v;
    G[cnt].next = head[u];
    head[u] = cnt;
    ++deg[v]; // 统计入度
}

int f[maxn], n, m; // f 为dp数组
bool flag[maxn]; // flag 表示在原图中入度是否为 0

int toposort() {
    queue<int> q;
    for (int i = 1; i <= n; i++) {
        if (deg[i] == 0)
        {
            flag[i] = true;
            f[i] = 1;
            q.push(i);
        }
    }
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        for (int i = head[u]; i; i = G[i].next)
        {
            int v = G[i].to;
            f[v] += f[u];
            if (--deg[v] == 0) q.push(v);
        }
    }
    int ans = 0;
    for (int i = 1; i <= n; i++)
    {
        if (head[i] == 0 && !flag[i]) ans += f[i];
    }
    return ans;
}

int main() {
    scanf("%d%d", &n, &m);
    int u, v;
    for (int i = 1; i <= m; ++i) {
        scanf("%d%d", &u, &v);
        addEdge(u, v);
    }
    printf("%d\n", toposort());
    return 0;
}